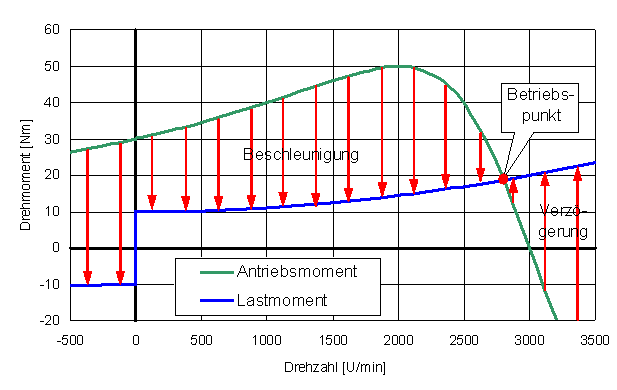
Bei der Dimensionierung eines Antriebssystems geht es darum, einen Antrieb zu finden, welcher eine Last im gewünschten Betriebsbereich betreiben kann. Damit ein Antrieb eine Last bewegen kann, muss er mehr Drehmoment als sie haben. Wenn er weniger hat, dann bewegt die Last den Antrieb oder das System bleibt im Stillstand. Wenn beide Kräfte (Drehmomente) gleich gross sind, befindet sich das System im Betriebspunkt.
Dieser Betriebspunkt kann genau dem Nennpunkt (Nenndrehzahl, Nenndrehmoment, Nennleistung) des Antriebes entsprechen, das wäre aber Zufall. Wenn der Antrieb für längere Zeit mehr Drehmoment abgeben muss, als er darf, wird er zu heiss und kann ausfallen. Dieses Thema wird im Beitrag "Thermische Antriebsauslegung" behandelt. Die Bestimmung der Lastmomente wird im Kapitel "Statische Antriebsauslegung" behandelt. Wenn die Bewegung in einer bestimmten Zeit erfolgen soll, ist zusätzlich die Masse (Schwungmasse) der beteiligten Systeme bei der Antriebsauslegung zu berücksichtigen. Dieses Thema wird im Kapitel "Dynamischen Antriebsauslegung" behandelt, welches auch die Transformation durch Getriebe und Umlenksysteme (Zahnstange, Riemen, Spindeln ...) beinhaltet. Im Beitrag "Positionierung" werden zusätzlich standardisierte Bewegungsabläufe aufgeführt.
Statische Antriebsauslegung
Basis der Antriebsdimensionierung ist die statische Antriebsauslegung. Es gilt die Bedingung, dass über den ganzen Drehzahlbereich das Lastmoment nicht grösser als das Antriebsmoment sein darf. Die Berechnung der Beschleunigung, der Einbezug von Getrieben und Umlenkeinrichtungen wird unter dynamischer Antriebsaulegung behandelt.
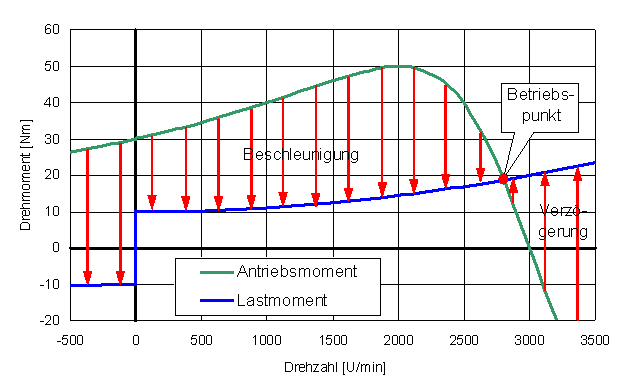
Lastkennlinien
Die Grundlage einer statischen Antriebsauslegung ist die Drehmoment-Drehzahlkennlinie der anzutreibenden Last. Man unterscheidet zwischen:
- hyperbolisches Lastmoment = konstante Leistung (spanabhebende Bearbeitung wie Bohren, Fräsen, Drehen und Zentrumswickler)
- konstantes Lastmoment bei Reibung (Gleitreibung) mit umgekehrtem Drehmoment bei negativen Drehzahlen und Hubarbeit (Kran, Lift ...) mit dem gleichen Drehmoment bei negativen Drehzahlen
- lineares Lastmoment, welches eher selten vorkommt (laminare Strömung, hydrodynamische Lager ...)
- quadratisches Lastmoment (turbulente Strömung zum Beispiel bei Lüfter und Pumpen)
- beliebiges, prozessspezifisches Lastmoment (Presse, Extruder ...)
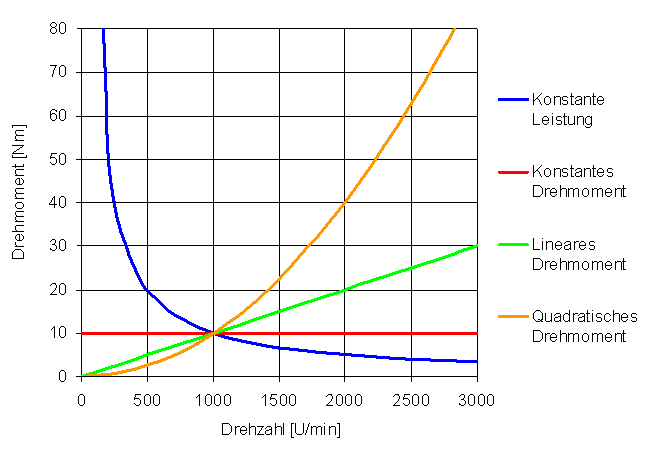
Bestimmung der Lastmomente
Die Bestimmung der Lastmomente kann in der Praxis recht aufwendig werden, ist aber für eine seriöse Antriebsauslegung notwendig. Die Vorgehensweise wird im folgenden stichwortartig beschrieben:
- Berechung der Prozesskräfte: Rechenmodell (siehe Beispiel Fahrzeugkräfte), Grundlagen aus Literatur (Dubbel, Papers ...); Computersimulation, Graphische Auswertung, Abschätzung und Vergleich aus bekannten ähnlichen Prozessen
- Messung der Kräfte und Bewegungen: Kraft- und Drehmomentmessgeräte (Messung der Gegenkraft), Bewegungsanalyse mit Videokamera (Kinematik), Messung mit Waage, Drehmoment = Kraft mal Hebellänge
- Messung über Motor an bestehender Maschine: Kalibrierung mit Drehmomentmessung, Aufzeichnung des momentbildenden Stromes, Rückrechnung zum Prozess Losbrechmoment
Anlauf
Ein spezieller Fall ist das erforderliche Drehmoment um eine Last aus dem Stillstand in Bewegung zu versetzen. Wenn das Losbrechmoment (die Haftreibung) deutlich kleiner als das Anzugsdrehmoment des Motors ist, sind keine Anlaufschwierigkeiten zu erwarten.
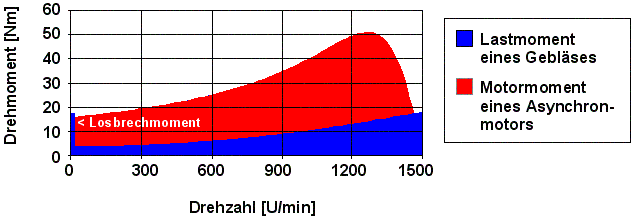
Bei hohen Haftmomenten nützt bei Asynchronmotoren ein Sanftanlaufgerät nicht viel, denn der Motor beschleunigt erst, wenn er genug Spannung hat, um das Losbrechmoment zu überwinden. In der Sternschaltung steht nur ein Drittel des Anlaufmomentes der Dreieckschaltung zur Verfügung. Mit einem modernen Frequenzumrichter steht aber schon beim Start ein hohes Drehmoment zur Verfügung.
Ein Asynchronmotor, der direkt oder mit einen Softstarter ans Netz geschaltet wird, erhitzt sich beim Hochfahren mit der Energie, welche der Rotationsenergie des Rotors und der Last entspricht. In den Datenblättern von Standardmotoren ist die zulässige Anzahl Leerumschaltungen pro Stunde angegeben. Kleine Asynchronmotoren können viel mehr Schaltungen (einige pro Sekunde) als grosse (einige pro Stunde) verkraften. Beim Betrieb mit einem Frequenzumrichter hat der Motor einen beschränkten Schlupf und kann viel häufiger gestartet werden.
Wenn das Lastdrehmoment unterhalb der Nenndrehzahl grösser als das Nenndrehmoment des Motors ist (Zentrumswickler, Knetmaschinen, Exzenter ...), so ist ein Antriebssystem mit einer Kennlinie zu suchen, welches diesen Bereich abdeckt (Gleichstrom-Reihenschluss-Motor, fremderregter Gleichstrom-Motor mit Feldschwächung, Asynchronmotor mit Frequenzumrichter in der Feldschwächung, geschalteter Reluktanzmotor). Als Alternative bleibt eine veränderbare Getriebeuntersetzung oder eine entsprechende Überdimensionierung des Antriebssystems.
Der Preis eines Motors hängt von seiner Grösse und somit vom Nenndrehmoment ab. Die Drehmomentanpassung an die Last ist mit einem Getriebe meistens günstiger als mit einem grossen Motor. Ein Getriebe hat ein Reibungsmoment, welches von der übertragenen Leistung wenig abhängig ist. Der Wirkungsgrad eines Motors oder eines Getriebes bezieht sich auf die Nennleistung. Im Teillastbereich oder bei tieferen Drehzahlen ist der Wirkungsgrad schlechter.
Leistung
Die Leistung \(P\) [W] rechnet sich aus Drehmoment \(M\) [Nm] mal Drehzahl \(\varOmega\) [rad/s] :
\(P = M \cdot \varOmega\)
Dabei ist zu beachten, dass für die Drehzahl nicht die übliche technische Grösse \(n\) [U/min] sondern die Grösse \(\varOmega\) [rad/s] benutzt wird. Teilweise wird für die Drehzahl auch das kleine Omega \(\omega\) verwendet. In der Elektrotechnik wird dieses kleine Omega aber auch für die Netzdrehfrequenz verwendet, darum wird hier für die Drehzahl das grosse Omega genommen. Für die Umrechnung gilt: 1 rad/s = (60 s/min) / (\(2 \cdot \pi\) rad/U) = 30 / 3.14 U/min = 9.55 U/min. Die üblicherweise verwendete Einheit für die Drehzahl \(n\) [U/min] ist etwa 10 mal grösser als die Grösse \(\varOmega\) [rad/s].
Ein Motor gibt nur seine Nennleistung ab, wenn die Last genau diese erfordert. Praktisch ist es unwahrscheinlich dass in einer Anwendung der Motor mit seiner Nennleistung belastet wird. Meistens ist das Lastmoment tiefer als das Nennmoment des Motors. Wenn einem Motor über längere Zeit mehr Drehmoment abverlangt wird, als er dauernd abgeben kann, wird er zu warm und kann ausfallen.
Dynamische Antriebsauslegung
Als Ergänzung zu den Anforderungen bei der statischen Antriebsauslegung muss bei der dynamischen Antriebsauslegung eine bestimmte Drehzahl oder Position in einer vorgegebenen Zeit erreicht werden. Für die dazu notwendige Beschleunigung (oder Verzögerung) muss das Antriebssystem ein zusätzliches Drehmoment aufbringen. Je grösser die Beschleunigung ist, desto mehr Kraft ist erforderlich. In vielen dynamischen Maschinen braucht der Motor die meiste Kraft, um seinen eigenen Rotor zu beschleunigen.
Translation: lineares System
Das translatorische System bezieht sich auf geradlinige (lineare) Bewegungen, wie sie Schlitten, Aufzüge, Kolben und andere Teile von Maschinen und Anlagen ausführen.
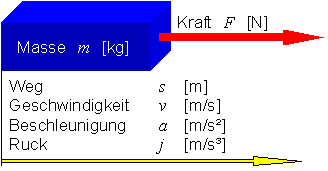
Die Grundeinheiten für das translatorische System sind der Weg \(s\) [m], die Zeit \(t\) [s] und die Masse \(m\) [kg]. Die Beschleunigungskraft ist \(F=\frac{\mathrm{d}(v \cdot m)}{\mathrm{d}t}\) [N (Newton) = kg m/s²]. Für nicht veränderliche Massen, ist die Beschleunigungskraft das Produkt aus Masse mal Beschleunigung: \(F = a \cdot m\).
Die Geschwindigkeit ist Weg durch Zeit: \(v=\frac{\mathrm{d}s}{\mathrm{d}t}\) [m/s], die Beschleunigung ist Geschwindigkeit durch Beschleunigungszeit: \(a=\frac{\mathrm{d}v}{\mathrm{d}t}\) [m/s²]. Im freien Fall mit einer Beschleunigung von etwa 10 m/s² nimmt die Geschwindigkeit pro Sekunde um 10 m/s (36 km/h) zu. Für die Beschreibung höherwertiger Bewegungsverläufe gibt es noch die Ableitung der Beschleunigung mit der Bezeichnung "Ruck": \(j=\frac{\mathrm{d}a}{\mathrm{d}t}\) [m/s³]. Im Beitrag Positionierung werden optimale Bewegungsabläufe für minimale Geschwindigkeit, minimale Beschleunigung und minimale Leistung dargestellt.
Rotation: drehendes System
Das rotative System bezieht sich auf Drehbewegungen wie sie in rotierenden elektrischen Maschinen, Getrieben, Walzen, Spindeln und Teilen von Maschinen und Anlagen vorkommen.

Die beste Einheit für den Winkel ist [rad], Radiant genannt. 1 rad = \(\frac{\text{1 Umdrehung}}{2 \cdot \pi}\) (0.16 Umdrehungen oder 57.3 Grad). Radiant ist eine dimensionslose Grösse, damit aber in der Rechnung das Bezugssystem deklariert wird, ist es nützlich die Einheit [rad] zu benutzen. Durch die Verwendung dieser Grösse können die Umrechnungsfaktoren bei der Berechnung weggelassen werden. Die Grundeinheiten für ein rotatives System sind der Winkel \(\varphi\) [rad], daraus lassen sich die Winkelgeschwindigkeit (Drehzahl) \(\varOmega=\frac{\mathrm{d}\varphi}{\mathrm{d}t}\) [rad/s], die Winkelbeschleunigung \(\alpha=\frac{\mathrm{d}\varOmega}{\mathrm{d}t}\) [rad/s²], der Winkelruck \(\sigma=\frac{\mathrm{d}\alpha}{\mathrm{d}t}\) [rad/s³] ableiten. Im rotativen System gibt es noch das Beschleunigungsmoment \(M\) [Nm] und die Schwungmasse (polares Massenträgheitsmoment) \(J\) [kgm²].
Bei der dynamischen Auslegung von Gelenken, Kurbeltrieben und ähnlichen Systemen ist bei der Berechnung der Beschleunigungsmomente die ausführliche Formel zu verwenden. Durch den veränderlichen Radius für die Bewegungsübertragung vom linearen ins rotative System verändert sich die transformierte Schwungmasse mit dem Winkel und der Zeit: \(M=\frac{\mathrm{d}(J \cdot \varOmega)}{\mathrm{d}t}=\alpha \cdot J + \varOmega \cdot \frac{\mathrm{d}(J)}{\mathrm{d}t}\) oder bei konstanter Schwungmasse vereinfacht \(M = \alpha \cdot J\).
Schwungmasse und Getriebe
Das polare Massenträgheitsmoment (Schwungmasse) eines Körpers nimmt quadratisch mit dem Abstand der Masse vom Rotationszentrum zu: \(J=\int r^2 \cdot \mathrm{d}m\). Bei einem Vollzylinder rechnet sich die Schwungmasse \(J\) [kgm²] aus dem Radius \(r\) [m] der Länge \(l\) [m], der Masse \(m\) [kg] und diese aus den Abmessungen und dem homogenem spezifischem Gewicht \(\rho\) [kg/m³] nach der Formel: \(J=\frac{1}{2} \cdot m \cdot r^2 = \frac{1}{2} \cdot \rho \cdot \pi \cdot l \cdot r^4\). Die Schwungmasse eines Vollzylinder nimmt also mit der vierten Potenz des Durchmessers zu. Ein um 20 % dickerer Zylinder hat die doppelte Schwungmasse.
Wenn zwei rotierende Körper über ein Getriebe miteinander verbunden sind, so wird die Schwungmasse mit dem Quadrat des Übersetzungsverhältnisses \(i\) [-] transformiert. Eine optimale Anpassung ist gefunden, wenn die transformierte träge Masse der Last gleich gross ist, wie die des Motors.
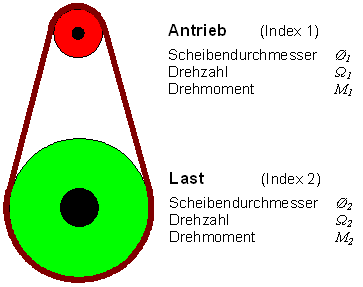
Die Transformation von Winkel, Drehzahl, Winkelbeschleunigung, Drehmoment und Schwungmasse durch ein Getriebe mit der Untersetzung \(i\) ist:
| Grösse | Antrieb | Last | |
|---|---|---|---|
| Winkel | \(\varphi_1\) | \(=\) | \(\varphi_2 \cdot i\) |
| Winkelgeschwindigkeit (Drehzahl) | \(\varOmega_1\) | \(=\) | \(\varOmega_2 \cdot i\) |
| Winkelbeschleunigung | \(\alpha_1\) | \(=\) | \(\alpha_2 \cdot i\) |
| Winkelruck | \(\sigma_1\) | \(=\) | \(\sigma_2 \cdot i\) |
| Drehmoment | \(M_1\) | \(=\) | \(M_2/i\) |
| Schwungmasse (resultierend) | \(J_{\text{res}}\) | \(=\) | \(J_1+J_2/i^2\) |
| Leistung | \(P_1\) | \(=\) | \(P_2\) |
Transformation: Umwandlung Translation in Rotation
Die Umwandlung einer rotativen in eine translatorische Bewegung kann auf verschiedene Arten erfolgen: Kette, Zahnriemen, Seilzug, Zahnstange, Spindel, usw. Bei diesen Transformationen kann ein Rechnungsradius \(r\) [m] als Umrechnungswert angenommen werden. Bei den Übertragungselementen mit einer Abwicklung über den Umfang entspricht dieser Radius dem geometrischen Wert. Bei einer Spindel ist der Rechnungsradius die Spindelsteigung \(s_p\)[m] durch 2 \(\pi\), die Spindelsteigung entspricht dem Umfang der "Seiltrommel". Bei der Formel für die resultierende Schwungmasse \(J_{\text{res}}\) [kgm²] bezogen auf die Seiltrommel ist zu beachten, dass die Masse \(m\) [kg] über den Seilzug direkt am Umfang der Seiltrommel angreift. Dadurch entfällt der Faktor \(\frac{1}{2}\), welcher bei der Berechnung der Schwungmasse bei einem Vollzylinder verwendet wird. Dort ist die Masse über das ganze Volumen gleichmässig verteilt.
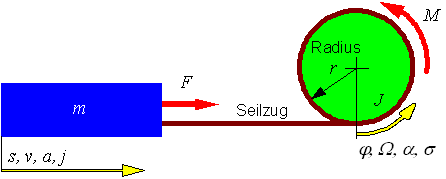
Die Transformation mit dem "Rechnungsradius" \(r\) ist:
| Grösse | Rotation | Translation | |
|---|---|---|---|
| Winkel | \(\varphi\) | \(=\) | \(s/r\) |
| Winkelgeschwindigkeit (Drehzahl) | \(\varOmega\) | \(=\) | \(v/r\) |
| Winkelbeschleunigung | \(\alpha\) | \(=\) | \(a/r\) |
| Winkelruck | \(\sigma\) | \(=\) | \(j/r\) |
| Drehmoment | \(M\) | \(=\) | \(F \cdot r\) |
| Schwungmasse (resultierend) | \(J_{\text{res}}\) | \(=\) | \(J+m \cdot r^2\) |
Energie und Leistung
Die Energie ist das Integral der Leistung über die Zeit. Für die Berechnung der Hochlaufzeit bei einer Beschleunigung mit konstanter Leistung (Feldschwächbereich einer Asynchronmaschine) kann über die Differenz der kinetischen Energie berechnet werden. Mit einer Kontrollrechnung über die Energie oder Leistung kann auch die Rechnung bei verknüpften Systemen (Getriebe, Zahnriemen ...) überprüft werden, indem jedes System einzeln gezählt wird.
| Grösse | Symbol | Einheit | Translation | Rotation |
|---|---|---|---|---|
| Leistung | \(P\) | W | \(F \cdot v\) | \(M \cdot \varOmega\) |
| Energie | \(W\) | J=Ws | \(\int P \cdot \mathrm{d}t\) | \(\int P \cdot \mathrm{d}t\) |
| Energie (statisch) | \(W\) | J | \(\int F \cdot \mathrm{d}s\) | \(\int M \cdot \mathrm{d}\varphi\) |
| Energie (Kraft/Moment konstant) | \(W\) | J | \(F \cdot s\) | \(M \cdot \varphi\) |
| Energie (kinetisch/dynamisch) | \(W\) | J | \(\frac{1}{2} \cdot m \cdot v^2\) | \(\frac{1}{2} \cdot J \cdot \varOmega^2\) |
| Energie (potentiell) | \(W\) | J | \(m \cdot g \cdot h\) | |
| Erdbeschleunigung | \(g\) | m/s² | 9.81 | |
| Höhenunterschied | \(h\) | m |