Die Dimensionierung von Transformatoren erfolgt über die magnetische Flussdichte im Eisen und die elektrische Stromdichte im Leiter. Die dauernd übertragbare Scheinleistung ist Nennspannung mal Nennstrom.
Spannungsanpassung: Die induzierte Spannung in der Primärwicklung ist die Veränderung der Flussdichte mal Anzahl Windungen mal Eisenquerschnittsfläche. Bei einem sinusförmigen Fluss ist die Ableitung der Flussdichte gleich gross wie die Kreisfrequenz mal die Flussdichte. Bei gegebener Flussdichte und Frequenz nimmt mit zunehmendem Eisenquerschnitt die erforderliche Anzahl Primärwindungen ab, was sich gut auf die Stromdichte in den elektrischen Leitern auswirkt. Je höher die Frequenz ist, desto kleiner wird der Transformator, je höher die Spannung ist, desto mehr Windungen sind erforderlich.
| Symbol | Einheit | Bezeichnung | Beziehungen |
|---|---|---|---|
| Φ | Vs | Magnetischer Fluss | |
| N | - | Anzahl Windungen | |
| AFe | m² | Eisenquerschnitt | |
| B | T | Magnetische Flussdichte | B = Φ / AFe |
| t | s | Zeit | |
| f | Hz | Frequenz | |
| ω | 1/s | Kreisfrequenz | ω = 2 π f |
| U | V | Elektrische Spannung | U(t) = N dΦ / dt |
| U(t) = N AFe dB / dt | |||
| U = N AFe ω B |
In der letzten obenstehende Beziehung gelten die Effektivwerte für die Spannung und Magnetische Flussdichte. In der Literatur wird die letzte Gleichung meistens mit der Frequenz, dem Multiplikator 4.44 (Pi mal Wurzel 2) geschrieben und für die Magnetische Flussdichte der Spitzenwert verwendet.
Stromanpassung: Der Nennstrom ergibt sich aus der zulässigen Stromdichte, dem zur Verfügung stehenden Querschnitt für die Leiter und der Anzahl Windungen. Je mehr Windungen erforderlich sind, desto geringer wird der zulässige Nennstrom. Wenn der zur Verfügung stehende Querschnitt vergrössert wird, nimmt die Länge des magnetischen Flusses im Eisen zu, was dann oft mit einem grösseren Eisenquerschnitt aufgeführt wird, was wiederum eine Anpassung der Windungszahl erforderlich macht.
| Symbol | Einheit | Bezeichnung | Beziehungen |
|---|---|---|---|
| J | A/m² | Stromdichte | |
| N | - | Anzahl Windungen | |
| ACu | m² | Kupferquerschnitt | |
| I | A | Elektrischer Strom | I = ACu J / N |
Beispiel für eine Dimensionierung
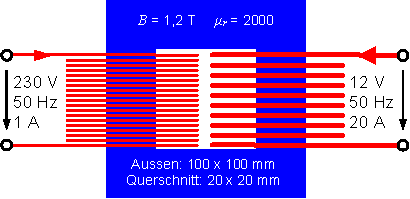
Für den obenstehenden Transformator gelten folgende Daten:
| Angabe | Rechnung | Bezeichnung | Wert | Bemerkung |
|---|---|---|---|---|
| U1 | Primärspannung | 230 V | Wird auch Nennspannung genannt | |
| I1 | Primärstrom | 1.1 A | Wird auch Nennstrom genannt | |
| S1 | = U1 I1 | Primärleistung | 253 VA | Entspricht bei grösseren Transformatoren der Nennleistung |
| U2 | Sekundärspannung | 12 V | ||
| I2 | Sekundärstrom | 20 A | ||
| S2 | = U2 I2 | Nennleistung | 240 VA | Sekundärleistung (Spannung mal Strom) |
| f | Nennfrequenz | 50 Hz | ||
| ω | = f 2 π | Kreisfrequenz | 314 1/s | |
| B | Nenninduktion | 1.2 T | Effektivwert, meistens wird der Maximalwert angegeben | |
| AFe | Geometrie | Eisenquerschnitt | 0.0004 m² | |
| lFe | Geometrie | Eisenlänge | 0.32 m | Rechteckiger Magnetflusspfad in der Mitte |
| μr | Relative Permeablität | 2000 | Eisenfüllfaktor eingerechnet | |
| μ | = μr μ0 | Permeabilität | 0.0025 Vs/Am | |
| σ | Streuung | 0.01 | ||
| γF | Spezifische Eisenverluste | 6 W/kg | bei 1,2 T Effektivwert und 50 Hz | |
| ρFe | Spezifisches Gewicht des Eisens | 7800 kg/m³ | Eisenfüllfaktor eingerechnet | |
| ACu | Geometrie | Wicklungsfenster | 0.0015 m² | Primär und Sekundär gleich gross |
| lCu | Geometrie | Wicklungslänge | 0.20 m | Rechteckiger Stromflusspfad in der Mitte |
| ρCu | Spezifischer Widerstand des Kupfers | 20 10-9 Ωm | bei einer Temperatur von 60 °C | |
| fCu | Füllfaktor Kupfer | 0.5 | ||
| S | Stromdichte im Leiter | 2 106 A/m² | Geringe Belastung für einen kleinen Trafo mit 2 A/mm² |
Bestimmung Anzahl der Primär- und Sekundärwindungen sowie die Drahtquerschnitte
| Bezeichnung | Beziehung | Rechnung | Ergebnis |
|---|---|---|---|
| Anzahl Primärwindungen | N1 = U1 / (AFe B ω) | = 230 V / (0,0004 m² 1.2 Vs/m² 314 1/s) = 1526 | 1530 |
| Anzahl Sekundärwindungen | N2 = N1 U2 / U1 | = 1530 12 V / 230 V = 79.8 | 80 |
| Leiterquerschnitt Primärwicklung | ACu1 = fCu ACu / N1 | = 0.5 0.0018 m² / 1530 = 0.588 10-6 m² | 0.5 mm² |
| Leiterquerschnitt Sekundärwicklung | ACu2 = fCu ACu / N2 | = 0.5 0.0018 m² / 80 = 11.3 10-6 m² | 10 mm² |
| Bemerkung: Die zulässige Stromdichte von 2 A/mm² wird eingehalten | |||
Bestimmung der Grössen des Ersatzschaltbildes
| Bezeichnung | Beziehung | Rechnung | Ergebnis |
|---|---|---|---|
| Widerstand der Primärwicklung | RCu1 = ρCu lCu N1 / ACu1 | = 20 10-9 Ωm 0.20 m 1530 / 0.5 10-6 m² = 12.2 Ω | 12 Ω |
| Widerstand der Sekundärwicklung | RCu2 = ρCu lCu N2 / ACu2 | = 20 10-9 Ωm 0.20 m 80 / 10 10-6 m² = 32.0 mΩ | 33 mΩ |
| Induktivität der Primärwicklung | L1 = N1² / (lFe / (AFe μ)) | = (1530)² / (0.32 m / (0.0004 m² 0.0025 Vs/Am)) = 7.35 H | 7.4 H |
| Induktivität der Sekundärwicklung | L2 = N2² / (lFe / (AFe μ)) | = (80)² / (0.32 m / (0.0004 m² 0.0025 Vs/Am)) = 20.1 mH | 20 mH |
| Hauptinduktivität | Lh = L1 / (1 - σ) | = 7.4 H (1 - 0.01) = 7.33 H | 7.3 H |
| Streuinduktivität der Primärwicklung | Lσ1 = L1 σ | = 7.4 H 0.01 = 74 mH | 74 mH |
| Streuinduktivität der Sekundärwicklung | Lσ2 = L1 σ | = 20 mH 0.01 = 0.20 mH | 200 μH |
| Eisenverluste | PvFe = γFe ρFe lFe AFe | = 6 W/kg 7800 kg/m³ 0.32 m 0.0004 m² = 5.99 W | 6 W |
| Ersatzwiderstand für die Eisenverluste | RFe = U1² / PvFe | = (230 V)² / 6 W = 8.82 kΩ | 8.8 kΩ |
Daraus ergibt sich untenstehendes Ersatzschaltbild.
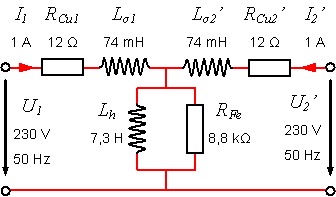
Das Ersatzschaltbild für den Transformator hat 2 Unzulänglichkeiten:
- keine galvanischen Trennung zwischen der Primär- und Sekundärwicklung
- keine Transformation mit dem Übersetzungsverhältnis 1530 / 80 = 19.13. Das wird mit getrichenen Grössen ['] auf der Sekundärseite korrigiert:
| Beziehung | Rechnung | Ergebnis |
|---|---|---|
| U2' = U2 ü = U1 | = 12 V 19.13 = 229.6 V | 230 V |
| I2' = I2 / ü = I1 | = 20 A / 19.13 = 1.05 A | 1.1 A |
| RCu2' = RCu2 ü² ≈ RCu1 | = 33 mΩ (19.13)² = 12.1 Ω | 12 Ω |
| Lσ2' = Lσ2 ü² ≈ Lσ1 | = 0.20 mH (19.13)² = 73.2 mH | 74 mH |
| Z2' = Z2 ü² | Für alle Impedanzen. welche an der Sekundärwicklung angeschlossen werden | |
Bestimmung der Betriebsdaten wie Nennleistung, Leerlaufstrom, Wirkungsgrad sowie Kurzschlussstrom
| Bezeichnung | Beziehung | Rechnung | Ergebnis | Bemerkung |
|---|---|---|---|---|
| Nennleistung | S2 = U2 I2 | = 12 V 20 A = 240 VA | 240 VA | a |
| Magnetisierungsstrom | Iμ = U1 / j ω Lh | = 230 V / (314 s-1 7.4 H) = 0.099 A | 100 mA | b |
| Eisenverluststrom | IFe = U1 / RFe | = 230 V / 8.8 kΩ = 0.0261 mA | 26 mA | c |
| Leerlaufstrom | I0 = √(IFe² + Iμ²) | = √((0.026 A)² + (0.1 A)²) = 0.1033 mA | 103 mA | d |
| Verluste bei Nennstrom | Pv = PvFe + 2 PvCu1 = PvFe + 2 RCu1 I1² | = 6 W + 2 12 Ω (1 A)² = 30 W | 30 W | |
| Nennwirkungsgrad | η = P / (P + Pv) | = 240 W / (240 W + 30 W) = 0.889 | 89% | e |
| Verluste bei Halblast | Pv50% = PvFe + 2 RCu1 (I1 0.5)² | = 6 W + 2 12 Ω (1 A 0.5)² = 12 W | 12 W | f |
| Wirkungsgrad bei Halblast | η50% = P50% / (P50% + Pv50%) | = 120 W / (120 W + 12 W) = 0.909 | 91% | |
| Kurzschlussstrom | I1k≈ U1 / (2 √(RCu1² + (ω Lσ1)²)) | = 230 V / (2 √((12 Ω)² + (314 s-1 0.074 H)²)) = 4.4 A | 4.4 A | g |
| Kurzschlussspannung | Uk = U1 I1 / I1k | = 230 V 1 A / 4.4 A = 52 V | 52 V | h |
| Bezogene Kurschlussspannung | uk = εc = Uk / U1 | = 52 V / 230 V | 23% | i |
Bemerkungen:
- Die Transformatorbelastung (zulässige Kupfer- und Eisenverluste) ist unabhängig von der übertragenen Wirkleistung, somit ist die Nenngrösse eines Transformators die Scheinleistung, also unabhängig vom Leistungsfaktor cosφ).
- Der Spannungsabfall über den Leiterwiderstand und die Streuinduktivität ist im allgemeinen zu vernachlässigen (0.1 A 26 Ω = 2.6 V gegenüber 230 V).
- Leerlaufstrom durch den Ersatzwiderstand für die Eisenverluste.
- Der Magnetisierungsstrom durch die Hauptinduktivität ist dominant.
- Bei der Berechnung des Wirkungsgrades wird mit einer ohmischen Last belastet, damit Wirkleistungen miteinander verglichen werden können.
- Der Wirkungsgrad ist belastungsabhängig, im Leerlauf ist der Wirkungsgrad 0%, weil keine Leistung übertragen werden und die Eisenverluste doch vorhanden sind
- Der Kurzschlussstrom ist 4.4 mal grösser als der Nennstrom. Der Spannungsabfall über die Streuinduktivität ist vor allem bei grösseren Transformatoren dominant
- Das heisst, dass bei einem sekundärem Kurzschluss und einer Eingangsspannung von 52 V der Nennstrom von 1 A fliesst
- Dimensionslose Angabe der Weichheit eines Transformators
Korrektur des Übersetzungsverhältnisses
Bei einem Primärstrom von 4.4 A ist die Sekundärspannung 0 V (Kurzschluss). Das heisst, dass beim Nennstrom von 1 A die Sekundärspannung nicht 12 V sondern um 23% tiefer bei 9.3 V liegt. Damit die Sekundärspannung bei übertragener Nennleistung den gewünschten Wert von 12 V hat, müssen mehr Sekundärwindungen eingebaut werden. Wenn dieser Transformator mit einer angepassten Sekundärwicklung im Leerlauf betrieben wird, liegt die Spannung an den Sekundärklemmen bei etwa 15.6 V, das Übersetzungsverhältnis ist von 19.1 auf 14.8 gesunken.

