Windturbinen können theoretisch nur einen Wirkungsgrad von 59 %  erreichen. Dieses gegen die Intuition gehende Resultat folgt aus dem  Gesetz von Betz und ist eine Folge der Tatsache, dass die Luft hinter der Turbine nicht still stehen kann.

Eine simpler Herleitung des Wirkungsgrades von Windturbinen findet sich in Beitrag Das Gesetz von Betz.

Annahmen

Wie für alle Herleitungen in der Physik braucht es ein Model. In diesem Fall wird ein unendlich dünner Rotor in einer Flüssigkeit (Luft wird hier als Flüssigkeit betrachtet) angenommen, die sich mit einer bestimmten Geschwindigkeit senkrecht zum Rotor bewegt.

Da die Geometrie des Rotors offensichtlich entscheidend ist, nehmen wir ausserdem an, dass dieser Rotor eine Scheibe ist (idealer Rotor), welche die Energie des Windes aufnimmt. Somit trifft der Wind mit einer Geschwindigkeit \(v_1\) auf die Scheibe, wird abgebremst und hat, nach Abgabe von Energie an die Scheibe, noch die Geschwindigkeit \(v_2\).

Zur einfacheren Berechnung, wird die Luft als inkompressibles Fluid betrachtet. Somit gibt es keinen Wärmetransfer.

Turbinenleistung

Zuerst berechnen wir die theoretische Turbinenleistung aus der Erhaltung der Masse (keine Luftteilchen gehen verloren). \(\mathrm{d}m_1\) sei die Masse eines (variablen) Volumens vor dem Rotor, \(\mathrm{d}m\) direkt beim Rotor und \(\mathrm{d}m_2\) nach dem Rotor. Die Erhaltung der Masse besagt:

\(\mathrm{d}m_1=\mathrm{d}m=\mathrm{d}m_2\)

Die Masse kann auch anderst geschrieben werden:

\(\mathrm{d}m = \mathrm{d}V \cdot \rho = A \cdot \mathrm{d}x \cdot \rho = A \cdot \frac{ \mathrm{d}x}{\mathrm{d}t}\mathrm{d}t \cdot \rho= A \cdot v \cdot \mathrm{d}t \cdot \rho\)

Dies entspricht der Masse eines Fluids mit Dichte \(\rho\) und Geschwindikeit \(v\) welches in der Zeit \(\mathrm{d}t\) eine Fläche \(A\) durchströmt.

Somit ergibt sich der konstante Massenstrom:

\(\dot{m}=\frac{\mathrm{d}m}{\mathrm{d}t}= A \cdot v \cdot \rho= A_1 \cdot v_1 \cdot \rho= A_2 \cdot v_2 \cdot \rho\)

Die Kraft des Massenelementes auf den Rotor entspricht:

\(-F =\mathrm{d}m \cdot a= \mathrm{d}m \cdot \frac{\mathrm{d}v}{\mathrm{d}t}= \dot{m} \cdot \mathrm{d}v\)

Integriert von \(v_1\) nach \(v_2\) ergibt dies (\(\dot{m}\) konstant):

\(F = - \dot{m} \cdot (v_2-v_1) =\dot{m} \cdot (v_1-v_2)=A \cdot v \cdot \rho\cdot (v_1-v_2) \)

Die Turbinenleistung lässt sich dann mit der Energiegleichung \(\mathrm{d}E=F \cdot \mathrm{d}x\) und der Beziehung zwischen Leistung und Energie \(P=\frac{\mathrm{d}E}{\mathrm{d}t}\) schnell berechnen (ME steht für Massenerhaltung):

\(P_{\text{ME}} = \frac{\mathrm{d}E}{\mathrm{d}t} = F \cdot \frac{\mathrm{d}x}{\mathrm{d}t} = F \cdot v =A \cdot v^2 \cdot \rho\cdot (v_1-v_2)\)          (1)

Weiter kann man die reale Turbinenleistung aus dem Energieunterschied des Windes vor und nach der Turbine berechnen. Dabei wird die Energieerhaltung verwendet.

\( \mathrm{d}E=\mathrm{d}E_{kin,v_1} - \mathrm{d}E_{kin,v_2} = \frac{1}{2} \cdot \mathrm{d}m \cdot ({v_1}^2-{v_2}^2)\)

Die Leistung berechnet sich dann zu (EE steht für Energieerhaltung):

\(P_{\text{EE}}=\frac{ \mathrm{d}E}{\mathrm{d}t} = \frac{1}{2} \cdot \frac{\mathrm{d}m}{\mathrm{d}t} \cdot ({v_1}^2-{v_2}^2)=\frac{1}{2} \cdot A \cdot v \cdot \rho \cdot ({v_1}^2-{v_2}^2)\)        (2)

Gleichung (1) und (2) wurden aus Massenerhaltung und Energieerhaltung hergeleitet. Beide sind demnach korrekt. Gleichsetzen führt zur Erkenntnis, dass für \(v\) die durchschnittliche Geschwindigkeit verwendet werden kann:

\(P=A \cdot v^2 \cdot \rho\cdot (v_1-v_2)=\frac{1}{2} \cdot A \cdot v \cdot \rho \cdot ({v_1}^2-{v_2}^2)\)

\( v\cdot (v_1-v_2)=\frac{1}{2} \cdot ({v_1}^2-{v_2}^2)=\frac{1}{2} \cdot ({v_1}-{v_2}) \cdot ({v_1}+{v_2})\)

Woraus folgt:

\( v=\frac{1}{2} \cdot ({v_1}+{v_2})\)

Damit kann die Turbinenleistung auf folgende Form gebracht werden:

\(P=\frac{1}{4} \cdot A \cdot \rho \cdot ({v_1}+{v_2}) ({v_1}^2-{v_2}^2)\)         (3)

Theoretische Turbinenleistung

Die theoretische Turbinenleistung ergibt sich, wenn man die Leistung des Windes vor der Turbine berechnet:

\(P_0=\frac{\mathrm{d}E_{kin,v_1}}{\mathrm{d}t}=\frac{1}{2} \cdot \frac{\mathrm{d}m}{\mathrm{d}t} \cdot {v_1}^2=\frac{1}{2} \cdot A \cdot \rho \cdot {v_1}^3\)

Wirkungsgrad

Der Wirkungsgrad ergibt sich dann zu:

\(\frac{P}{P_0}=\frac{1}{2}\frac{({v_1}+{v_2}) \cdot ({v_1}^2-{v_2}^2)}{{v_1}^3}\)

Durch Umformen und verwenden der Ersetzung \(x=\frac{v_2}{v_1}\) (relative Geschwindigkeitsänderung) nimmt der Wirkungsgrad folgende Form an:

\(\frac{P}{P_0}=\frac{1}{2}(1+x-x^2-x^3)\)

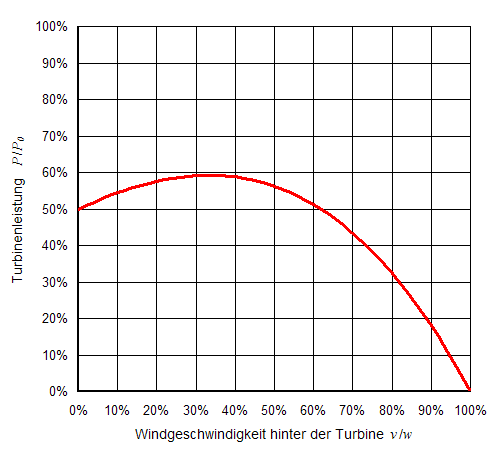
Das Maximum dieser Funktion lässt sich durch Ableiten nach x und Nullsetzen bestimmen.

\(\frac{\mathrm{d}}{\mathrm{d}x} \frac{P}{P_0}=\frac{1}{2}(1-2x-3x^2)=0\)

Aufgelöst nach \(x\):

\(x_{1,2}=\frac{-2 \pm \sqrt{4+12}}{6}=-1, \, \frac{1}{3}\)

Lösungen eingesetzt in den Wirkungsgrad:

\({(\frac{P}{P_0})}_{\text{min,max}}=\frac{1}{2}(1+x-x^2-x^3)=0, \, \frac{16}{27}\)

Somit ist der theoretisch mögliche maximale Wirkungsgrad einer Windturbine 59.3%.