Die Berechnung des Drehmoments einer Asynchronmaschine erfolgt hier über untenstehendes vereinfachtes einphasiges Ersatzschaltbild. Bei dieser Berechnung werden die Sättigung, die Eisenverluste und die Stromverdrängung in den Rotornuten vernachlässigt. Beim Drehmoment in Funktion der Spannung und Frequenz wird auch der Widerstand der Statorwicklung vernachlässigt.
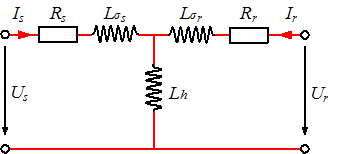
Maschengleichung für den Statorkreis und den Rotorkreis |
|||
| Us | = | Rs Is + j ωs Ls Is + j ωs Lh Ir | Ls = Lσs + Lh |
| Ur | = | Rr Ir + j ωr Lr Ir + j ωr Lh Is | Lr = Lσr + Lh |
| = | 0 | Rotorwicklung kurzgeschlossen | |
| . | |||
Berechnung des Rotorstroms |
|||
| Ir | = | - j ωr Lh Is / (Rr + j ωr Lr) | |
| = | - j ωr Lh Is x / (ωr Lr + j ωr Lr x) | x = ωr Lr / Rr | |
| = | - j Lh Is x / (Lr (1 + j x) | ||
| = | - j Lh Is x (1 - j x) / (Lr (1 + x²)) | ||
| = | - Lh Is x (j + x) / (Lr (1 + x²)) | ||
| . | |||
Einsetzen des Rotorstroms in die Maschengleichung des Statorkreises |
|||
| Us | = | Rs Is + j ωs Ls Is - j ωs Lh Lh Is x (j + x) / (Lr (1 + x²)) | |
| = | Rs Is + j ωs Ls Is - j ωs (1- σ) Ls Is x (j + x) / (1 + x²) | σ = 1 - Lh² / (Ls Lr) | |
| = | (Rs + j ωs Ls + ωs (1- σ) Ls x (1 - j x) / (1 + x²)) Is | ||
| . | |||
Berechnung der Wirkleistung des Statorkreises eines Stranges |
|||
| Ps | = | Us Is* | Imaginärteil fällt weg |
| = | (Rs + ωs (1- σ) Ls x / (1 + x²)) Is² | ||
| . | |||
Berechnung der Verlustleistungen eines Stranges |
|||
| Pv | = | Rs Is² + Rr Ir² | |
| = | Rs Is² + Rr (- Lh Is x (j + x) / (Lr (1 + x²)))² | ||
| = | Rs Is² + (Rr Lh² x² (j + x)² / (Lr (1 + x²))²) Is² | ||
| = | Rs Is² + (ωr Lh² x (j + x)² / (Lr (1 + x²)²)) Is² | Rr = ωr Lr / x | |
| = | Rs Is² + (ωr (1- σ) Ls x (j + x)² / (1 + x²)²) Is² | Lh² = (1 - σ) Ls Lr | |
| = | Rs Is² + (ωr (1- σ) Ls x (1 + x²) / (1 + x²)²) Is² | Berechnung des Betrages | |
| = | (Rs + ωr (1- σ) Ls x / (1 + x²)) Is² | ||
| . | |||
Berechnung der mechanischen Leistung eines Stranges |
|||
| Pm | = | Ps - Pv | |
| = | (Rs + ωs (1- σ) Ls x / (1 + x²)) Is² - (Rs + (ωr (1- σ) Ls x / (1 + x²)) Is² | ||
| = | ((ωs - ωr) (1- σ) Ls x / (1 + x²)) Is² | ||
| . | |||
Berechnung der mechanischen Drehzahl, Definition des Schlupfes |
|||
| Ω | = | (ωs - ωr) / p | p = Polpaarzahl (1 für 2-polig) |
| Ω0 | = | ωs / p | Synchrone Drehzahl (Leerlauf) |
| s | = | ωr / ωs | Schlupf |
| = | (Ω0 - Ω) / Ω0 | ||
| . | |||
Berechnung des Drehmoments aus dem Statorstrom |
|||
| M | = | m Pm / Ω | m = Strangzahl (3 für 3-phasig) |
| M | = | m p (1- σ) Ls x / (1 + x²) Is² | Drehmoment |
| . | |||
Berechnung der Statorimpedanz |
|||
| Zs | = | Us / Is | |
| = | Rs + j ωs Ls + ωs (1- σ) Ls x (1 - j x) / (1 + x²) | ||
| = | (j (1 + x²) + (1- σ) x (1 - j x)) ωs Ls / (1 + x²) | für Rs << ωs Ls | |
| = | ((1- σ) x + j (1 + x² - (1- σ) x²)) ωs Ls / (1 + x²) | ||
| = | ((1- σ) x + j (1 + σ x²)) ωs Ls / (1 + x²) | ||
| Zs² | = | ((1- σ)² x² + (1 + σ x²)²) ωs² Ls² / (1 + x²)² | |
| = | (x² - 2 σ x² + σ² x² + 1 + 2 σ x² + σ² (x²)²) ωs² Ls² / (1 + x²)² | ||
| = | (1 + x²) (1 + σ² x²) ωs² Ls² / (1 + x²)² | ||
| = | (1 + σ² x²) ωs² Ls² / (1 + x²) | ||
| . | |||
Berechnung des Drehmoments aus der Statorspannung |
|||
| M | = | m p (1- σ) Ls x / (1 + x²) Us² / Zs² | |
| = | m p (1- σ) Ls x / (1 + x²) Us² / ((1 + σ² x²) ωs² Ls² / (1 + x²)) | ||
| M | = | m p (1- σ) x / (Ls (1 + σ² x²)) Us² / ωs² | Drehmoment |
| . | |||
Berechnung des Kippmomentes und Kippschlupfes |
|||
| M’ | = | dM / dx | |
| ~ | 1 / (1 + σ² x²) - 2 σ² x² / (1 + σ² x²)² | ||
| 0 | = | 1 + σ² x² - 2 σ² x² | Bedingung für Kippmoment |
| xk | = | 1 / σ | |
| Mk | = | m p (1- σ) / (Ls σ (1 + σ² / σ²)) Us² / ωs² | Kippdrehmoment |
| Mk | = | m p (1- σ) / (2 σ Ls) Us² / ωs² | Kippmoment |
| xk | = | ωrk Lr / Rr | |
| ωrk | = | Rr / (σ Lr) | Rotorkippfrequenz |
| sk | = | Rr / (σ ωs Lr) | Kippschlupf |


