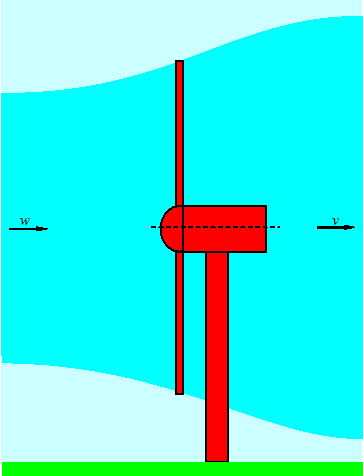
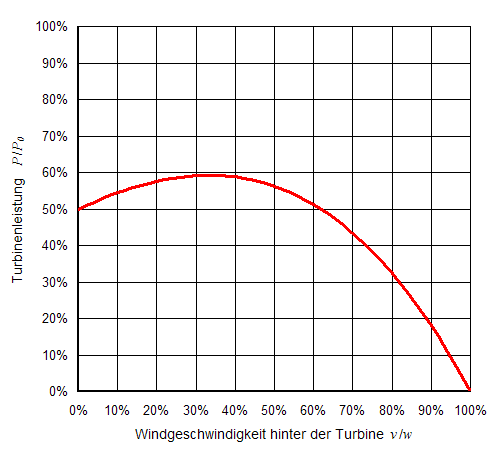
Die Leistung einer Windturbine hängt vom Abbremsen der Luft ab. Ist die Windgeschwindigkeit hinter der Turbine tief, dann hat man viel Kraft, aber wenig Massendurchsatz. Ist die Windgeschwindigkeit hinter der Turbine hoch, hat man wenig Kraft, aber viel Massendurchsatz. Das Optimum kann man aus der Ableitung der entsprechenden Funktion finden.
Herleitung
| \(P_0 = \rho \, A \, \frac{w^3}{2}\) |
Theoretische Turbinenleistung des Windes mit Dichte \(\rho\) durch Rotorfläche \(A\) mit Geschwindigkeit \(w\). Einheit: \([\text{W}]\) Leistung bei voller Ausnützung der translatorischen Energie des Windes. Aus der Masse des Windes \(m = V \rho = A w t \rho\) eingesetzt in \(E_{\text{kin}}=\frac{1}{2}m w^2 =\frac{1}{2}A t \rho w^3\) und unter Verwendung der kinetischen Leistung des Windes ergibt sich die theoretische Turbinenleistung \(P_0 = \frac{E_{\text{kin}}}{t}= \rho \, A \, \frac{w^3}{2}\) |
| \(\dot{m} = \rho \, A \, \frac{v + w}{2}\) |
Durchschnittlicher Massenstrom \([\frac{\text{kg}}{\text{s}}]\) Masse die sich pro Zeiteinheit durch einen Querschnitt bewegt. \(\frac{v + w}{2}\) bezeichnet dabei die durchschnittliche Geschwindigkeit. |
| \(P = \dot{m}\, \frac{w^2-v^2}{2} = \rho \, A \, \frac{v + w}{2} \, \frac{w^2-v^2}{2}\) |
Turbinenleistung \([\text{W}]\) Folgt aus dem Energieunterschied des Windes vor und nach der Turbine \(\Delta E=E_{\text{kin, w}} - E_{\text{kin, v}} = \frac{1}{2} \cdot m \cdot (w^2-v^2)\). Daraus ergibt sich die Turbinenleistung \(P =\frac{\Delta E}{\Delta t} = \dot{m}\, \frac{w^2-v^2}{2} = \rho \, A \, \frac{v + w}{2} \, \frac{w^2-v^2}{2}\)
|
Wem diese Herleitung zu schwammig ist, kann sich hier die physikalisch korrekte Herleitung anschauen.
Wirkungsgrad
Der Wirkungsgrad ergibt sich dann zu:
\(\frac{P}{P_0}=\frac{1}{2}\frac{({w}+{v}) \cdot ({w}^2-{v}^2)}{{w}^3}\)
Durch Umformen und verwenden der Ersetzung \(x=\frac{v}{w}\) (relative Geschwindigkeitsänderung) nimmt der Wirkungsgrad folgende Form an:
\(\frac{P}{P_0}=\frac{1}{2}(1+x-x^2-x^3)\)
Das Maximum dieser Funktion lässt sich durch Ableiten nach x und Nullsetzen bestimmen.
\(\frac{\mathrm{d}}{\mathrm{d}x} \frac{P}{P_0}=\frac{1}{2}(1-2x-3x^2)=0\)
Aufgelöst nach \(x\):
\(x_{1,2}=\frac{-2 \pm \sqrt{4+12}}{6}=-1, \, \frac{1}{3}\)
Lösungen eingesetzt in den Wirkungsgrad:
\({(\frac{P}{P_0})}_{\text{min,max}}=\frac{1}{2}(1+x-x^2-x^3)=0, \, \frac{16}{27}\)
Somit ist der theoretisch mögliche maximale Wirkungsgrad einer Windturbine 59.3%.

