Ursprünglich gab es nur Batterien und Gleichstrom, mit der Erfindung von Generatoren kamen Wechselstrom und Drehstrom dazu.

Gleichstrom

Mit Gleichstrom ist meistens eine Spannungsquelle gemeint, welche eine konstante Spannung (Gleichspannung) abgibt.

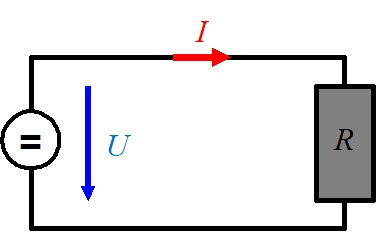
Beim Gleichstrom gibt es vier Grössen:

• \(U\) [V = Volt] Spannung
• \(I\) [A = Ampère] Strom
• \(R\) [Ω = Ohm] Widerstand
• \(P\) [W = Watt] Leistung

Die Grundbeziehungen lauten:

• \(U = R \cdot I\)
• \(P = U \cdot I\)

und daraus abgeleitet:

• \(P = R \cdot I^2\)
• \(P = U^2 / R\)

Für die Kombination mit mehreren Quellen und Widerständen gibt es zwei einfache Regeln:

• Maschenregel: In einem beliebig geschlossen Stromkreis ist die Summe der Spannung gleich Null.
• Knotenregel: In einem Verbindungspunkt ist die Summe der eintretenden und austretenden Ströme gleich Null.

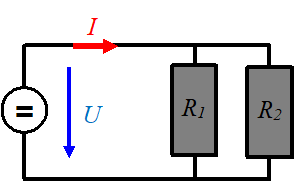
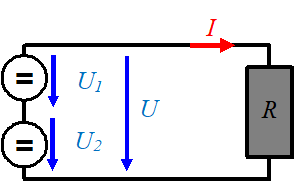
Stromversorgung mit Gleichstrom

Wenn man heute im Haushalt die elektrischen Geräte analysiert, dann stellt man fest, dass immer mehr Geräte intern mit Gleichstrom betrieben werden. Es stellt sich dann die Frage, warum gibt es überhaupt Wechselstrom? Es wäre doch einfacher, wenn es nur Gleichstrom gibt? Aber welche Spannung wäre dann die Richtige: 100 Volt für grosse Leistungen wie Kochherd oder Waschmaschine, 12 Volt wie im Auto für Lampen und Elektronik sowie 5 Volt für das Handy? Wenn man zum Beispiel 12 V wählt, dann würde ein Kochherd mit 2.4 Kilowatt Leistung einen Strom von 200 Ampère ziehen. Dafür sind nicht nur sehr dicke Kabel, sondern auch grosse Steckdosen und Stecker erforderlich. Auch schon ein Staubsauger mit 480 Watt Leistung erfordert bei 12 Volt einen Strom von 40 Ampère.

Der grosse Vorteil von Wechselstrom ist, dass man die Spannung mit Transformatoren beliebig anpassen kann. Die Elektrizität aus grossen Kraftwerken transportiert man mit hoher Spannung in die Agglomerationen. In den Hochspannungsleitungen fliesst so ein relativ kleiner Strom, dafür sind nur daumendicke Leiterquerschnitte nötig und es gibt auch nur geringe Übertragungsverluste. Die weitere Stromverteilung erfolgt dann über mehrere Hochspannungsstufen bis zur Wechselspannung im Haushalt mit den bei uns bekannten 230 Volt. Man könnte das heute auch mit Gleichstrom machen. Die dazu erforderlichen Spannungswandler benötigen Halbleiter, sie sind teurer, störungsanfälliger und haben einen schlechteren Wirkungsgrad.

Wechselstrom

Beim Wechselstrom gelten eigentlich die gleichen Regeln wie beim Gleichstrom. Beim Wechselstrom ist die Spannung aber nicht konstant, sondern sie verändert sich mit der Zeit. Der Wechselstrom wird fast ausschliesslich von Synchrongeneratoren erzeugt.

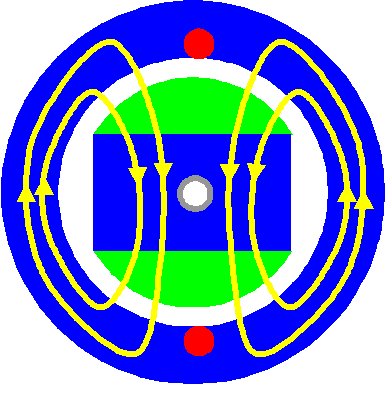
Im 2-poligen Synchrongenerator dreht sich ein Magnet 50 mal pro Sekunde. In der feststehenden Wicklung wird eine sinusförmige Spannung mit der Frequenz von 50 Hz induziert.

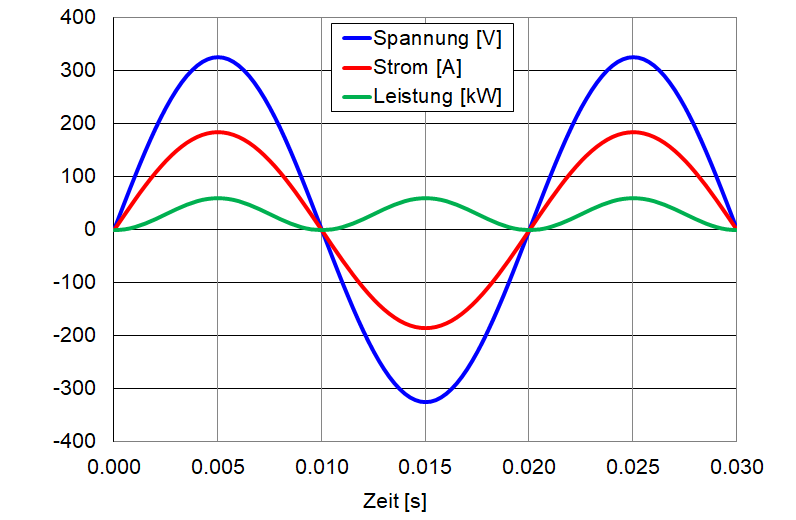
Im oberen Kurvenverlauf sieht man, dass im Zeitpunkt 0.000 und 0.010 Sekunden alle Werte Null sind. Man sieht auch, dass bei 0.005 Sekunden, bei der maximalen Spannung von 325 V ein maximaler Strom von 191 A (325 V / 1.7 Ω) fliesst, was eine maximale Leistung von 62 kW (325 V \(\cdot\) 191 A) ergibt. Bei 0.015 Sekunden sind Spannung und Strom negativ, die Leistung aber positiv. Die durchschnittliche Leistung beträgt die Hälfte der Spitzenleistung, hier 31 kW.

Damit die bekannten Beziehungen des Gleichstroms auch beim Wechselstrom gelten, verwendet man den Begriff Effektivwert. Bei sinusförmigen Grössen ist der Effektivwert um die Wurzel 2 (1.414) kleiner, als der Spitzenwert. Beim obigen Beispiel betragen die Effektivwerte 230 V,  135 A und 31 kW.

Beim Wechselstrom gibt es nicht nur den ohmschen Widerstand, sondern noch zwei weitere frequenzabhängige Widerstände, die Induktivität und die Kapazität, welche beide elektrische Energie speichern können.

Beim Wechselstrom gibt es folgende Grössen:

• \(U\) [V = Volt] Spannung, Effektivwert
• \(f\) [Hz = Herz] Frequenz, in Europa 50 Hz, in den USA 60 Hz
• \(I\) [A = Ampère] Strom, Effektivwert
• \(R\) [Ω = Ohm] Widerstand, auch ohmschen Widerstand genannt
• \(L\) [H = Henry = Ωs] Induktivität, meistens eine Art Spule
• \(C\) [F = Farad = Ω/s] Kapazität, als Bauteil ein Kondensator

Die Grundbeziehungen lauten:

• \(U = R \cdot I\)
• \(U = 2 π f L \cdot I\)
• \(I = 2 π f C \cdot U\)

Der Spannungsabfall über einer Induktivität nimmt mit der Frequenz zu, die Impedanz (der Wechselstromwiderstand) wird grösser. Bei Gleichstrom hat die Spule nach dem Aufbau ihres Magnetfeldes keinen Widerstand mehr, sie ist wie ein Kurzschluss. Bei der Kapazität ist es genau umgekehrt. Je höher die Frequenz, desto kleiner wird ihre Impedanz. Bei Gleichstrom fliesst nach dem der Kondensators geladen ist, kein Strom mehr durch die Kapazität.

Die Induktivität (Spule) und die Kapazität (Kondensator) können elektrische Energie speichern. Bei der Induktivität ist die Energie quadratisch zum fliessenden Strom, bei der Kapazität quadratisch zur angelegten Spannung.

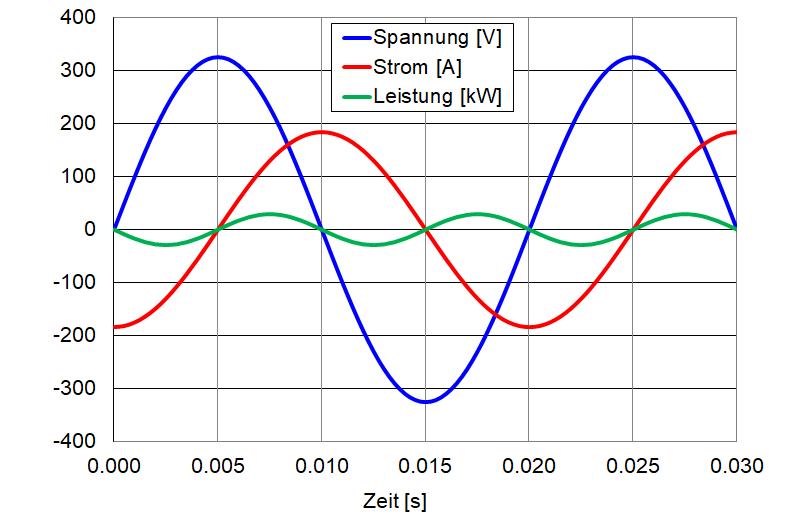
In der oberen Grafik sieht man, dass bei einer rein induktiven Last der Stromverlauf gegenüber dem Spannungsverlauf verschoben ist. Wenn man einer Periode (hier 0.020 Sekunden) eine volle Umdrehung und somit einem Winkel von 360 ° zuordnet, so beträgt der Winkel der Verschiebung 90 °. Diesen Winkel nennt man Phasenwinkel oder \(φ\) (phi), von dem dann meistens der Cosinus verwendet wird. Der Durchschnitt der Abgabeleistung beträgt in der Grafik Null Watt.

Bei einer entsprechenden rein kapazitiven Last (1.7 Ω, 1.87 mF) wäre der Stromverlauf invers, der Phasenwinkel \(φ\) - 90 °.

In Wirklichkeit gibt es keine reinen Widerstände, Induktivitäten oder Kapazitäten. Jede Leitung und jedes Bauteil hat etwas von allen 3 Eigenschaften. Praktisch aber meistens so wenig, dass man diese vernachlässigen kann.

Beim Wechselstrom gibt es nebst dem Phasenwinkel \(φ\) drei verschiedene Leistungen:

• \(φ\) [-] Phasenwinkel, der Verschiebewinkel zwischen Strom und Spannung.
• \(S\) [VA] Scheinleistung, die Leistung aus Produkt Strom mal Spannung.
• \(P\) [W = Watt] Wirkleistung, die Leistung welche wirklich verbraucht wird. In der Stromrechnung wird der Energieverbrauch in kWh (1 Kilowattstunde = 1000 Watt während 1 Stunde) verrechnet.
• \(Q\) [var] Blindleistung, die Leistung, welche zwischen Quelle und Last pendelt. Eine Induktivität bezieht nur Blindleistung, eine Kapazität gibt Blindleistung ab.

Die Grundbeziehungen lauten:

• \(S = U \cdot I\)
• \(P = \mathrm{cos}φ \cdot S\)
• \(Q = \mathrm{sin}φ \cdot S\)

sowie daraus abgeleitet:

• \(S^2 = P^2 + Q^2\)

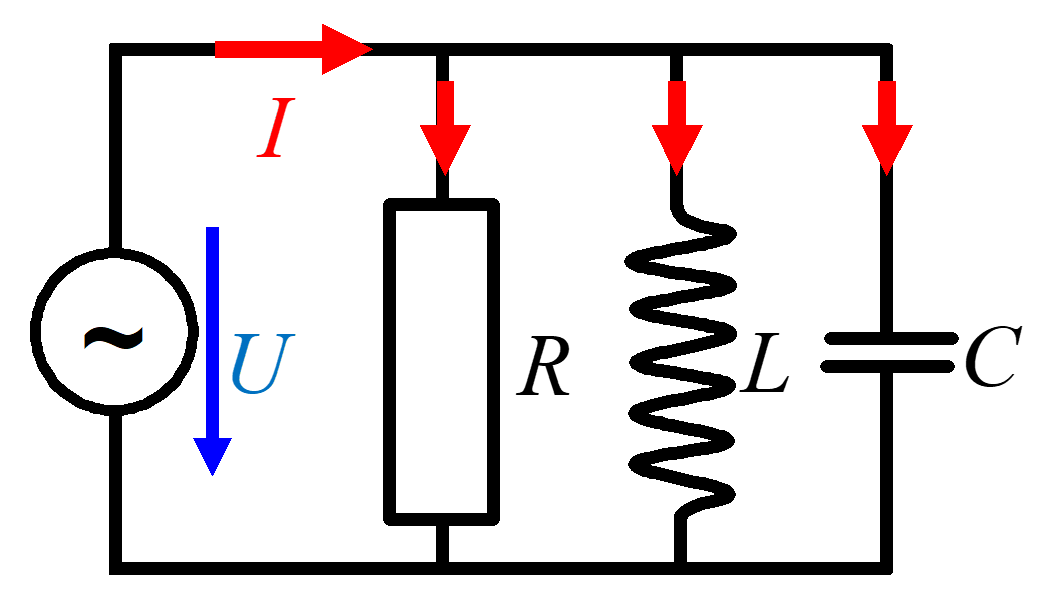
Beispiel für Wechselstrom

An einer 230 Volt Quelle werden nacheinander 3 verschiedenartige Lasten angeschlossen.

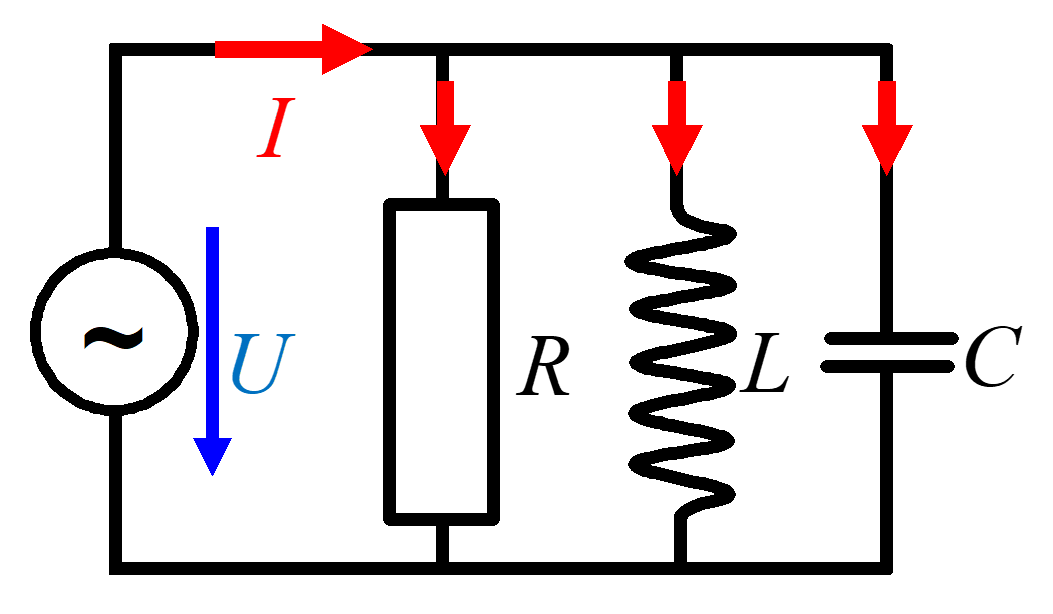
7 Fragen

1. Wie gross ist der Strom \(I\) wenn nur der Widerstand \(R\) mit 230 Ohm angeschlossen ist?
2. Wie gross ist der Strom \(I\) wenn nur die Induktivität \(L\) mit 0.73 Henry (entspricht einer Impedanz von 230 Ohm) angeschlossen ist?
3. Wie gross ist der Strom \(I\) wenn nur die Kapazität \(C\) mit 13.8 10^-6 Farad (entspricht einer Impedanz von 230 Ohm) angeschlossen ist?
4. Wie gross ist der Strom \(I\) wenn der Widerstand \(R\) und die Induktivität \(L\) angeschlossen sind.
5. Wie gross ist der Strom \(I\) wenn der Widerstand \(R\) und die Kapazität \(C\) angeschlossen sind.
6. Wie gross ist der Strom \(I\) wenn die Induktivität \(L\) und die Kapazität \(C\) angeschlossen sind.
7. Wie gross ist der  Strom \(I\) wenn alle drei Lasten angeschlossen sind.

Antworten

• Frage 1 bis 3 und 7 ergibt 1 A.
• Frage 4 und 5 ergeben 1.41 A. Der Widerstand bezieht Wirkleistung \(P\), die Induktivität oder Kapazität Blindleistung \(Q\). Die Ströme sind um 90 ° Phasenverschoben, man muss sie vektoriell addieren.
• Frage 6 ergibt 0 A. Die Ströme durch die Induktivität und Kapazität heben sich auf. Somit ergibt sich bei Aufgabe 7 die gleiche Lösung wie bei Aufgabe 1.