Messungen an Transformatoren

Die spezifischen Daten von Transformatoren können über Messungen oder über die Nachrechnung aus der Konstruktion abgeschätzt werden.

Abschätzung der Nenndaten

Wenn keine Nenndaten angegeben sind, kann bei einer angenommenen Frequenz (zum Beispiel 50 Hz) über die Aufnahme der Leerlaufkennlinie die Nennspannung abgeschätzt werden. Dazu wird mit einer veränderlichen Wechselspannungsquelle (Verstelltrafo, Variac) die Spannung von Null V aus kontinuierlich erhöht und zusammen mit dem Strom in einem Diagramm dargestellt. Meistens liegt die Nennspannung im Übergang zur Sättigung. Der Nennstrom kann aus dem Leiterquerschnitt der Primärwicklung abgeschätzt werden. Überschlagsmässig kann von etwa 10 A Strom pro mm² Leiterquerschnitt ausgegangen werden.

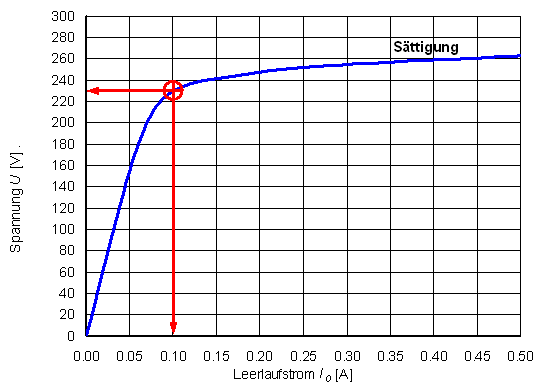
Messungen

Die einzelnen Werte des Ersatzschaltbildes eines Transformators können mit verschiedenen Messungen bestimmt werden.

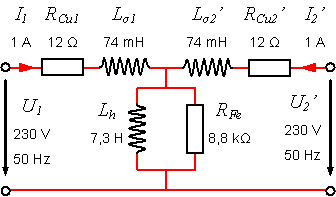
Widerstandsmessung

Der ohmsche Widerstand der Wicklungen R_Cu1 und R_Cu2 kann mit einem Ohmmeter gemessen werden. Bei grösseren Transformatoren sind die Widerstandswerte so klein, dass der Übergangswiderstand der Messklemmen eine grosse Rolle spielt. Nebst der Verwendung einer Messbrücke kann man einen Gleichstrom von zum Beispiel 1 A einspeisen und an den Transformatorklemmen die Spannung messen. Bei der Widerstandsmessung ist zu beachten, dass Temperaturkoeffizient von Kupfer 0.0039 1/K beträgt, bei 10 K Temperaturdifferenz sind das fast 4%.

Leerlaufmessung

Bei offenen Sekundärklemmen wird an die Primärwicklung die Nennspannung angelegt. Das Verhältnis der Primärspannung zur Sekundärspannung ergibt das Übersetzungsverhältnis: ü = U₁ / U₂. Das Spannungsverhältnis im Leerlauf ist auch das Verhältnis der Wicklungszahlen ü = N₁ / N₂

Der aufgenommene Leerlaufstrom I₀ teilt sich auf in den Magnetisierungsstrom I_μ und den Strom für die Eisenverluste I_Fe. Mit einer zusätzlichen Leerlaufleistungsmessung P₀ ≈ Pv_Fe [W] können diese beiden Ströme unterschieden werden: I_Fe = Pv_Fe / U₁ denn vor allem die Eisenverluste beziehen Wirkleistung (die Wirkleistungsaufnahme der Primärwicklung kann bei kleinen Leerlaufströmen im Verhältnis zum Nennstrom im allgemeinen vernachlässigt werden. Bei relativ grossen Leerlaufströmen können die Kupferverluste mit Pv_Cu1 = R_Cu1 I₀² von der Leerlaufleistung P₀ abgezogen werden, der ohmsche Widerstand R_Cu1 ist aus der Widerstandsmessung schon bekannt). Daraus lässt sich der Ersatzwiderstand für die Eisenverluste berechnen: R_Fe = U₁²  / Pv_Fe oder R_Fe = U₁ / I_Fe.

Mit der im Leerlauf aufgenommenen Blindleistung lässt sich nach dem gleichen Verfahren wie beim Eisenwiderstand der Strom durch die Hauptinduktivität berechnen: I_μ = Q₀ / U₁ und daraus die Primärinduktivität: L₁ = U₁ / (ω I_μ). Bei vielen Transformatoren ist die Streuinduktivität L_σ1 sehr viel kleiner als die Hauptinduktivität L_h, so dass L₁ ≈ L_h gesetzt werden kann. Wenn keine Blindleistungsmessung zur Verfügung steht, kann die Blindleistung aus der Scheinleistung und Wirkleistung errechnet werden: Q₀ = √(S₀² - P₀²).

Kurzschlussmessung

Bei kurzgeschlossenen Sekundärklemmen wird die Spannung an der Primärwicklung soweit erhöht, bis der Nennstrom fliesst. Wenn die Nennspannung angelegt würde, könnten die entstehenden Stromwärmeverluste in den Kupferdrähten den Transformator zerstören. Je höher diese Spannung U_1k im Verhältnis zur Nennspannung U₁ liegt, desto grösser ist die Streuung des Transformators. Je tiefer die relative Kurzschlussspannung liegt, desto grösser wäre der Kurzschlussstrom: I_1k =  I₁ U₁ / U_1k. Der Strom, welcher über die Hauptinduktivität I_μ und den Eisenwiderstand I_Fe fliesst, kann in den meisten Fällen vernachlässigt werden, da beim Kurzschluss nur etwa die halbe Eingangsspannung über diesen beiden Impedanzen anliegt. Der Kurzschlussstrom wird durch den ohmschen Widerstand R_Cu und die Streuinduktivität L_σ der beiden Wicklungen begrenzt. Da bei der üblichen Transformatorauslegung die Primärgrössen und transformierten Sekundärgrössen etwa gleich gross sind R_Cu2' = R_Cu2 ü² ≈ R_Cu1 und L_σ2' = L_σ2 ü² ≈ L_σ1, ergibt sich folgende Formel: 2 (R_Cu1 + jωL_σ1) = U_1k / I₁ und für die gesuchte Streuinduktivität: L_σ1 = √((U_1k / (2 I₁))² - R_Cu1²) / ω. Bei grösseren Transformatoren kann der Wicklungswiderstand oft vernachlässigt werden.