Unter Positionierung versteht man die Verschiebung einer Masse um eine Strecke in einer bestimmten Zeit. Zu Beginn und am Ende der Positionierung steht die Masse still, das heisst die Geschwindigkeit ist Null. Der Bewegungsverlauf kann beliebig erfolgen.
Für die Positionierung gibt es 3 Extremlösungen:
| Grösse | Minimale Geschwindigkeit | Minimale Beschleunigung | Minimale Leistung |
|---|---|---|---|
| Beschleunigungszeit | 0 | \(\frac{t_p}{2}\) | \(\frac{t_p}{3}\) |
| Maximale Geschwindigkeit | \(\frac{s}{t_p}\) | \(2 \cdot \frac{s}{t_p}\) | \(1.5\cdot\frac{s}{t_p}\) |
| Beschleunigung | \(\infty\) | \(4\cdot\frac{s}{t_p^2}\) | \(4.5\cdot \frac{s}{t_p^2}\) |
| Maximale Leistung | \(\infty\) | \(8 m \cdot \frac{s^2}{t_p^3}\) | \(6.25m\cdot \frac{s^2}{t_p^3}\) |
Verwendete Grössen:
| Grösse (rotativ) | Translatorisch | Rotativ | ||
|---|---|---|---|---|
| Symbol | Einheit | Symbol | Einheit | |
| Positionierzeit | \(t_p\) | s | \(t_p\) | s |
| Strecke (Winkel) | \(s\) | m | \(\varphi\) | rad |
| Geschwindigkeit (Winkelgeschwindigkeit) | \(v\) | m/s | \(\Omega\) | rad/s |
| Beschleunigung (Winkelbeschleungiung) | \(a\) | m/s² | \(\alpha\) | rad/s² |
| Masse (Schwungmasse) | \(m\) | kg | \(J\) | kgm² |
| Maximale Leistung | \(P\) | W | \(P\) | W |
Bei der Masse (Schwungmasse) ist die gesamte bewegte Masse (Last, Getriebe, Antrieb) zu berücksichtigen. Bei genauen Positionieraufgaben sollte die berechnete Positionierzeit etwas kürzer sein, als die zur Verfügung stehende Zeit, da das System oft noch ausschwingen muss. Eine weiterer Parameter ist dann die Berücksichtigung des Rucks (Veränderung der Beschleunigung). Bei zeitkritischen Anwendungen wird meistens die Bewegungsform mit minimaler Beschleunigung (die halbe Zeit Vollgas, die andere Hälfte Vollbremsung) gewählt. Wenn die Last (z.B. Reibung, Gewichtskraft ...) nicht zu vernachlässigen ist sollten diese Kräfte berücksichtigt werden, indem zum Beispiel für die Beschleunigung mehr Zeit zur Verfügung steht, weil die Reibung zum Beispiel beim Bremsen hilft.
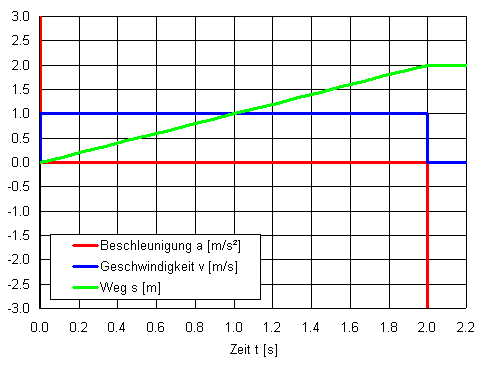
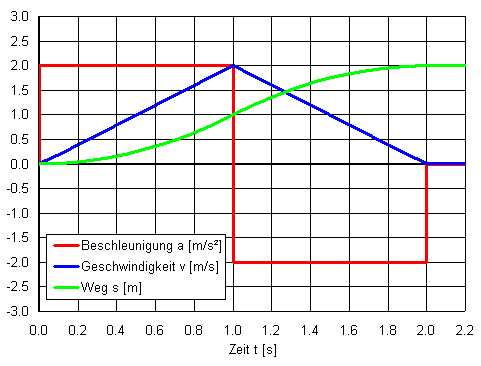
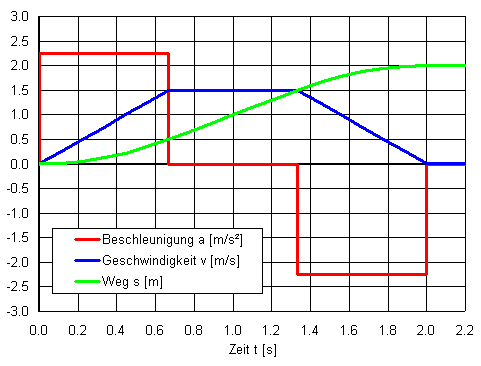
Diagramme
Für die Positionierung über eine Strecke \(s\) von 2 Meter innerhalb \(t_p\) von 2 Sekunden ergeben sich folgende 3 Extremlösungen: