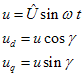Servoantrieb ist der Oberbegriff für einen Aktor, welcher sich für eine Positionierung eignet. Damit können pneumatische, hydraulische oder elektrische Antriebe gemeint sein. Oft ist damit eine Synchronmaschine mit Servoverstärker (besserer Umrichter) gemeint, welche auch als büstenlose Gleichstrommaschine (brushless DC-Drive = BLDC) bezeichnet wird. Üblicherweise wird sie mit einem Lagegeber (zum Beispiel Resolver) betrieben, hier sind aber auch Methoden ohne Lagegeber (sensorless) beschrieben.
\(\begin{array}{lcl}M &=& i \Psi \\ u &=& Ri+L \frac{\mathrm{d}i}{\mathrm{d}t}+\Omega \Psi \end{array}\)
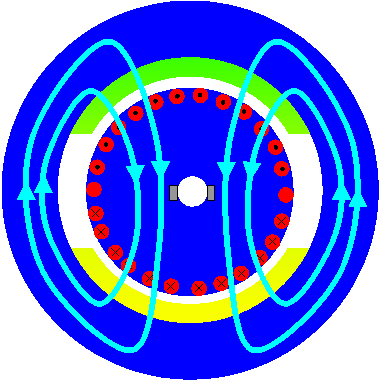
Permanenterregte Gleichstrommaschine.
|
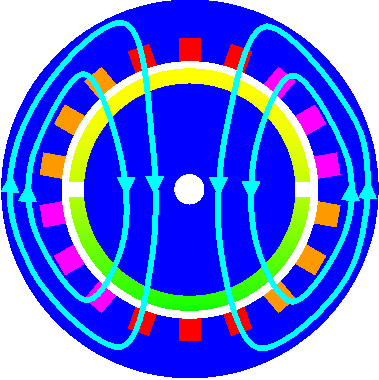
\(\begin{array}{lcl}M_{\left( \gamma \right)}&=& \frac{\partial W_{mag}}{\partial \gamma} \\ M &=& \frac{3}{2} p \left[ i_q \Psi_d + i_d \Psi_q \right] \\ u &=& Ri+L \frac{\mathrm{d}i}{\mathrm{d}t}+\Omega \Psi \end{array}\) Permanenterregte Synchronmaschine
|
Geregelte Synchronmaschine mit Lagegeber
| Struktur: | 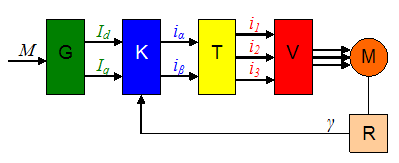 |
|---|---|
| Legende: | G Drehmomentrechner K Kommutierungsrechner T Transformation 2 zu 3 Phasen) V Stromregler (Frequenzumrichter) M Synchronmaschine R Resolver |
| Drehmoment: |
\(M=\frac{3}{2} p \left[ i_q \Psi_d + i_d \Psi_q \right]\) |
| Ströme: |
\(\begin{array}{lcl}i_\alpha &=& i_d \cos{\gamma} - i_q \sin{\gamma} \\ i_\beta &=& i_d \sin{\gamma} + i_q \cos{\gamma} \end{array}\) |
| Statorströme: |
\(\begin{array}{lcl}i_l &=& i_\alpha \\ i_2 &=& \frac{\sqrt{3}}{2} i_\alpha-\frac{1}{2}i_\beta \\ i_3 &=& -\frac{\sqrt{3}}{2} i_\alpha-\frac{1}{2}i_\beta \end{array}\) |
Geregelte Synchronmaschine ohne Lagegeber
Zur Regelung der Synchronmaschine ohne Lagegeber gibt es verschiedene Methoden:
1. Steuerung, Überwachung der Spannungen und Ströme
Grundprinzip: Kontrolle des Phasenwinkels zwischen Spannung und Strom
| Struktur: | 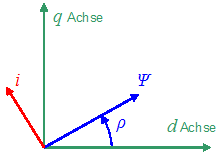 |
|---|---|
| Winkel: |
\(\rho =\tan^{-1}\left( \frac{\Psi_q}{\Psi_d} \right)\) |
| Flussverkettungen: |
\(\begin{array}{lcl}\Psi_d &=& \int \left( u_d-R i_d \right) \mathrm{d}t \\\Psi_q &=& \int \left( u_q-R i_q \right) \mathrm{d}t \end{array}\) |
| Spannungen: |
\(\begin{array}{lcl}u_d &=&\frac{1}{3} \left( u_{21}-u_{13} \right) \\ u_q &=& -\frac{1}{\sqrt{3}} \left( u_{21}+u_{13} \right) \end{array}\) |
| Ströme: |
\(\begin{array}{lcl}i_d &=& i_1 \\ i_q &=& -\frac{1}{\sqrt{3}} \left( i_1+2 i_2 \right) \end{array}\) |
2. Abschätzung über die dritte Oberwelle der Statorspannung
| Struktur: | 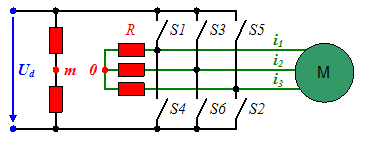 |
|---|---|
| Beziehungen: | \(\begin{array}{lcl}u_{\small{0}} &=& u_{\small{3^\prime}}+u_{\small{5^\prime,7^\prime \ldots}}=u_{\small{1}}+u_{\small{2}}+u_{\small{3}} \\ \Psi_{\small{3^\prime}} &=& \int u_{\small{3^\prime}} \mathrm{d}t \end{array}\) |
| Innere Spannugen und Ströme: | 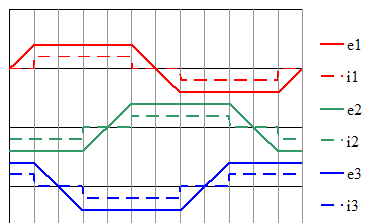 |
| 3. harmonische Oberwelle und Flussverkettung: |
 |
| Schalterstellungen: | 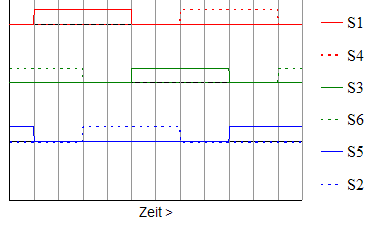 |
3. Abschätzung über die Rückwirkung der induzierten Spannung
- Erfassung des Nulldurchgangs der induzierten Spannung in der Phase, welche gerade nicht geschaltet ist.
- Integration der induzierten Spannung in der Phase, welche gerade nicht geschaltet ist.
- Erfassung des stromführenden Intervalls der Freilaufdioden
4. Abschätzung der Drehzahl und Position
- Analyse der Statorspannungen und der Statorströme mit Extended Kalman Filter …
5. Abschätzungen der Veränderung der Induktivität
- Erfassung der Rotorinduktivität, welche sich durch den Sättigungseffekt vom Magnetfeld des Rotors lageabhängig verändert
- Erfassung der Quer- und Längsreaktanz der rotorlageabhängigen Statorinduktivität
6. Abschätzungen durch künstliche Intelligenz
- Einsatz von künstlichen neuralen Netzwerken oder fuzzy Netzwerken
Transformation von 3 auf 2 Phasen und zurück
| 3 und 2 Achsen-System | Umwandlung mit Matrizen | |
|---|---|---|
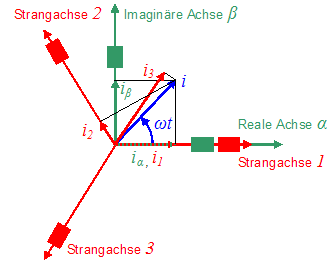 |
Umwandlung von 3 auf 2 Phasen | Umwandlung von 3 auf 2 Phasen |
| \(x_{\small{1,2,3}}=\mathbf{T} \, \mathbf{x}_{\small{a,b,0}}\) | \(x_{\small{a,b,0}}=\mathbf{T}^{\small{T}} \, \mathbf{x}_{\small{1,2,3}}\) | |
| \(\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\frac{2}{3} \cdot \begin{bmatrix}1 & 0 & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} & \frac{1}{2}\end{bmatrix} \cdot \begin{pmatrix}x_\alpha\\x_\beta\\x_0\end{pmatrix}\) | \(\begin{pmatrix}x_\alpha\\x_\beta\\x_0\end{pmatrix}=\begin{bmatrix}1 &- \frac{1}{2}& -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & - \frac{\sqrt{3}}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\end{bmatrix} \cdot \begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}\) | |
| \(\begin{array}{lcl}x_{\small{1}} &=& x_{\small{a}} \\ x_{\small{2}} &=& -\frac{1}{2}x_{\small{a}}+\frac{\sqrt{3}}{2}x_{\small{b}}\\ x_{\small{3}} &=& -\frac{1}{2}x_{\small{a}}-\frac{\sqrt{3}}{2}x_{\small{b}}\end{array}\) | \(\begin{array}{lcl}x_{\small{a}} &=& x_{\small{1}} \\ x_{\small{b}} &=& \frac{1}{\sqrt{3}}x_{\small{1}}+\frac{2}{\sqrt{3}}x_{\small{2}}\\ x_{\small{0}} &=&0\end{array}\) | |
Resolver
Der Resolver ist ein analoger Drehwinkelmesser für die Erfassung der Rotorposition.
| Struktur: | 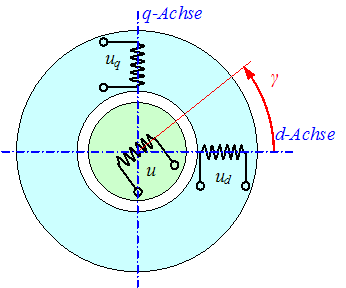 |
|---|---|
| Beziehungen: |
|
| Signal: | 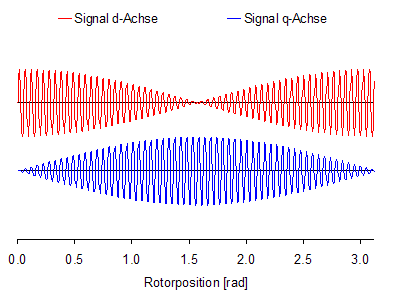 |
Literatur
- Peter Vas, Sensorless vector and direct torque control, Oxford University Press, 1998
- Klaus Hofer, Sensorlose Antriebsregelung, VDI Verlag, 1990