Boote mit einer Verdrängung von über 300 kg haben meistens einen Motor. Es gibt Boote mit schwachen Motoren (Flautenschieber), hochmotorisierte Boote und natürlich auch solche mit einer vernünftigen Motorisierung. Die passende Motorleistung ist aber nur ein Teil des Bootsantriebes, der Propeller (Schiffsschraube) muss auch passen.

Beispiel: Ein Propeller hat an dem einem Boot 65 % Wirkungsgrad, an einem andern nur noch 40 %.

In diesem Beitrag geht es um die Dimensionierung von Bootsantrieben für kleinere Segelyachten. Es wird erklärt, wie die Rumpfgeschwindigkeit und die dafür erforderliche Motorleistung bestimmt wird und wie ein optimaler Bootspropeller (Durchmesser und Steigung) ausgewählt wird.

Rumpfgeschwindigkeit

Wenn Boote durchs Wasser fahren, dann gibt es vom Bug aus Wellen die sich nach hinten fortpflanzen. Der Abstand dieser Wellen (die Wellenlänge) hängt von der Fahrtgeschwindigkeit ab. Es gilt folgende Beziehung:

\(l = {\dfrac{2 \cdot \pi}{g}} \cdot v^2\)

\(l\) = Wellenlänge in m
\(\pi\) = Kreiskonstante = 3.14
\(g\) = Erdbeschleunigung = 9.81 m/s²
\(v\) = Geschwindigkeit in m/s

Wenn die zweite Welle am Heck angekommen ist, fährt das Boot mit seiner Rumpfgeschwindigkeit. Diese lässt sich aus der vorangehenden Beziehung umformen:

\(v= {\sqrt({\dfrac{g}{2 \cdot \pi}} \cdot l)} = 1.25 \cdot \sqrt{l}\)

Die Rumpfgeschwindigkeit steigt mit der Wurzel aus der Wasserlinienlänge. Umgerechnet auf die übliche Geschwindigkeitsgrösse in km/h sind das:

\(v_R = 4.5 \cdot \sqrt{l_W}\)

\(v_R\) = Rumpfgeschwindigkeit in km/h
\(l_W\) = Wasserlinienlänge in m

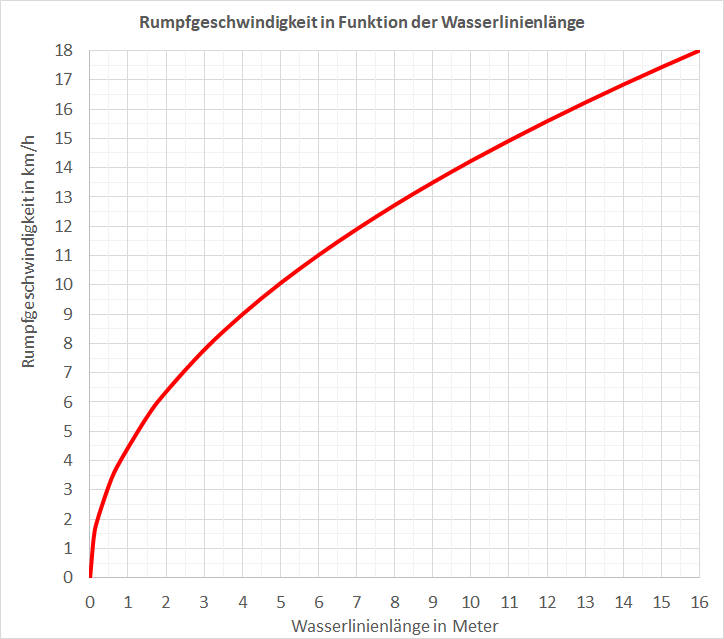
Bei reinen Verdränger (Boote, welche nicht ins Gleiten kommen) ist die Rumpfgeschwindigkeit die übliche maximale Geschwindigkeit. Höhere Geschwindigkeiten erfordern viel mehr Antriebsleistung, es wirken hohe Kräfte und das Boot kann in instabile Lagen geraten.

Motorleistung

Die erforderliche Motorleistung errechnet sich aus Widerstandskraft des Bootes mal Bootsgeschwindigkeit durch Wirkungsgrad des Propellers.

Die Widerstandskraft setzt sich aus zwei Komponenten zusammen:

• Der Reibungswiderstand hängt von der benetzten Oberfläche, ihrer Rauigkeit, der Form und dem Quadrat der Geschwindigkeit ab.
• Der Wellenwiderstand hängt von der verdrängten Wassermasse, der Form und von einer höheren Potenz der Geschwindigkeit ab.

Bis zu etwa einem Viertel der Rumpfgeschwindigkeit ist der Widerstand des Bootsrumpfs sehr klein. Bis zu etwa Dreiviertel der Rumpfgeschwindigkeit dominiert der Reibungswiderstand, danach der Wellenwiderstand. Bei Booten die ins Gleiten kommen, zum Beispiel Jollen oder leichte Yachten, nimmt die Zunahme des Wellenwiderstandes bei höherer Geschwindigkeit (etwa bei 7/6 der Rumpfgeschwindigkeit) ab. Für das Gleiten sorgt eine Rumpfform, welcher bei höheren Geschwindigkeit dynamischen Auftrieb erzeugt und das Boot aus dem Wasser hebt, wobei die benetzte Fläche auch kleiner wird.

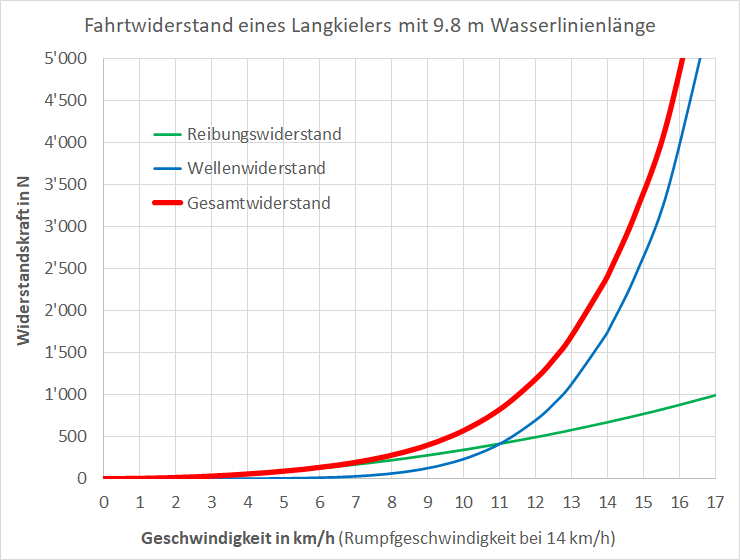
Fahrtwiderstand und Rumpfgeschwindigkeit nehmen mit zunehmender Bootslänge zu. Die erforderliche Motorleistung ist das Produkt dieser beiden Grössen durch den Propellerwirkungsgrad (im Durchschnitt etwa 65 %).

Faustformel für die Motorleistung von Booten bei Rumpfgeschwindigkeit:

\(P_M = 0.25 \cdot m \cdot l_W\)

\(P_M\) = Motorleistung in kW
\(m\) = Bootsgewicht in Tonnen (= verdrängtes Volumen in m³)
\(l_W\) = Wasserlinienlänge in m

Beispiel: Für ein Boot mit 6 m Wasserlinienlänge und 2 Tonnen Gewicht ergibt das einen Motor mit 3 kW Leistung.

Die gewählte Motorleistung kann auch geringer oder grösser ausfallen. In der folgenden Grafik sind Prospektdaten von verschiedenen Segelyachten dargestellt.

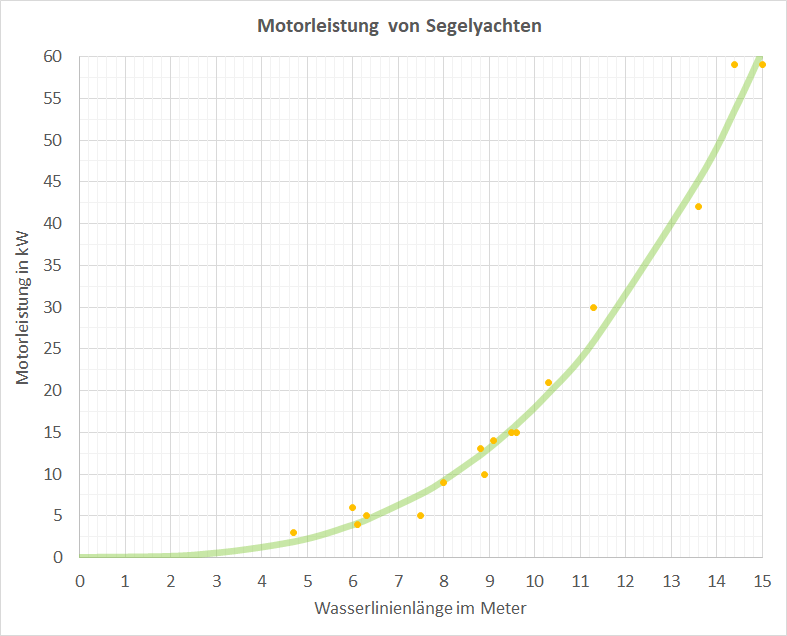
Den Fahrtwiderstand eines Bootes kann man auch messen. Man lässt sich schleppen und misst die Zugkraft an der Schlepptrosse und die Fahrtgeschwindigkeit. Die erforderliche Leistung ist Kraft in Newton mal Geschwindigkeit in m/s.

\(P_B = \frac{1}{1000} \cdot F \cdot v\)

\(P_B\) = Leistung für das Boot in kW
\(F\) = Zugkraft in N (Newton)
\(v\) = Geschwindigkeit in m/s

Umgerechnet auf die Kraftmessung mit einer Waage in kg und der Geschwindigkeit in km/h gibt es folgende Formel:

\(P_B = \frac{2.73}{1000} \cdot F_W \cdot v_K\)

\(F_W\) = Zugkraft in kp (Messung von kg mit Waage)
\(v_K\) = Geschwindigkeit in km/h

Beispiel: Ein Boot wird mit 11 km/h geschleppt, die Zugkraft beträgt 80 kg. Die berechnete Leistung für das Boot ergibt 2.4 kW.

Die erforderlich Motorleistung ist um den Propellerwirkungsgrad grösser.

\(P_M = \dfrac{100 %}{\eta} \cdot P_B\)

\(P_M\) = Motorleistung in kW
\(\eta\) = Propellerwirkungsgrad (50 bis 80 %, im Mittel etwa 65 %)

Beispiel: Bei einer Leistung für das Boot von 2.4 kW und einem Propellerwirkungsgrad von 65 % beträgt die Motorleistung 3.7 kW.

Hinweis: Bei einem Boot, welches mit dem eigenen Propeller angetrieben wird, ist der Fahrtwiderstand etwas anders als beim Schleppen. Die Strömung des Propellers beeinflusst den Bootswiderstand und die Strömung des Bootes beeinflusst den Propeller.

Propellerantrieb

Bei einer festen Drehzahl hat ein Propeller bei stillstehendem Boot (zum Beispiel an einen Pfahl belegt) die maximale Schubkraft. Mit zunehmender Fahrtgeschwindigkeit nimmt die Schubkraft ab.

Der Propeller erzeugt einen Wasserstrahl mit einer Geschwindigkeit, welche das Produkt aus Drehzahl und Propellersteigung ist. Der Durchmesser des Wasserstrahls ist proportional zum Propellerdurchmesser.

Damit der Propeller Schub auf das Boot abgeben kann, muss dieser Wasserstrahl schneller als das Boot sein. Die Abweichung zwischen Boots- und Strahlgeschwindigkeit nennt man Schlupf.

Beispiel: Fährt das Boot Strahlgeschwindigkeit, ist der Schlupf 0 %. Hat das Boot seine Nenngeschwindigkeit, liegt der Schlupf zwischen 10 bis 50 %. Liegt das Boot still, ist der Schlupf 100 %.

Propellerdiagramm

Auf Grundlage der Strahltheorie, welche am Schluss erklärt wird, lässt sich das untenstehende allgemeine Propellerdiagramm erstellen. Es ist unabhängig von Geschwindigkeit, Leistung, Propellerdurchmesser und Propellersteigung. Ausgemessenen oder genau berechneten Propeller weichen von diesem Diagramm etwas ab.

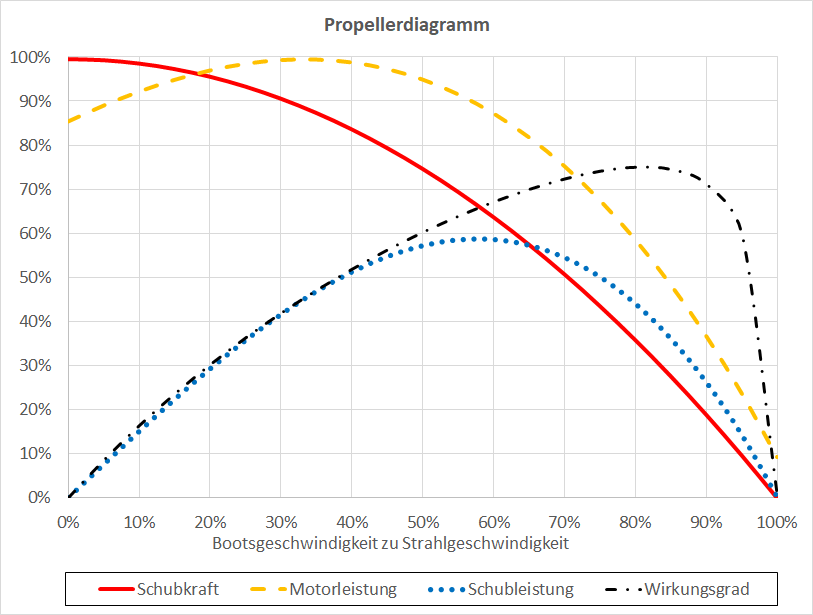
Die horizontale Achse zeigt die Bootsgeschwindigkeit im Verhältnis zur Strahlgeschwindigkeit. Der Schlupf ist die Differenz dieses Wertes zu 100 %.

Die rote Kennlinie ist die Schubkraft, hier im Maximum auf 100 % skaliert. Je mehr sich die Bootgeschwindigkeit der Strahlgeschwindigkeit nähert, desto kleiner wird die Schubkraft.

Die gepunktete blaue Kennlinie ist die Abgabeleistung des Propellers (Schubkraft man Bootsgeschwindigkeit). Im Stillstand ist sie 0 %, da die Bootsgeschwindigkeit auch 0 % ist. Beim Erreichen der Strahlgeschwindigkeit ist sie wieder 0 %, da die Schubkraft 0 % ist. Das Maximum der Abgabeleistung liegt bei etwa 60 % Bootsgeschwindigkeit durch Strahlgeschwindigkeit (40 % Schlupf).

Die gelb gestrichelte Kennlinie ist die Motorleistung (Drehmoment mal Drehzahl). In dieser Kennlinie wurde die Reibung des Propellers berücksichtigt, im dem die Motorleistung um 10 % gegenüber der Berechnung aus der Strahltheorie erhöht wurde. Im Stillstand beträgt die Motorleistung etwa 85 % vom Maximalwert. Dieser tritt bei 33 % vom Verhältnis Bootsgeschwindigkeit zu Strahlgeschwindigkeit auf (Schlupf 67 %). Bei höherer Bootsgeschwindigkeit und gleicher Drehzahl muss der Motor dann weniger Leistung abgeben. Daraus folgt: Ein Bootsantrieb, der zum Beispiel für 20 % Schlupf ausgelegt wurde, wird bei Vollgas und viel Gegenwind oder beim Schleppen überlastet, seine Drehzahl sinkt.

Die schwarze Strichpunkt Kennlinie zeigt den Wirkungsgrad des Propellers (Abgabeleistung durch Motorleistung). Der beste Propellerwirkungsgrad von 75 % liegt bei 80 % des Verhältnis Bootsgeschwindigkeit zu Strahlgeschwindigkeit (Schlupf 20 %). Bei 50 % Schlupf ist der Wirkungsgrad immer noch 60 %.

Die hier beschriebenen Werte basieren auf der Strahltheorie und 10 % Reibungsverluste. Reale Propeller haben leicht andere Werte.

Kraft-Geschwindigkeit-Kennlinie

Im untenstehenden Diagramm ist ein Beispiel der Kraft-Geschwindigkeit-Kennlinie des Bootes und des Propellerantriebes eingezeichnet. Dort wo sich diese beiden Kurven schneiden, stellt sich die Fahrtgeschwindigkeit ein. Darunter wird das Boot mit der Differenz dieser beiden Kräfte beschleunigt.

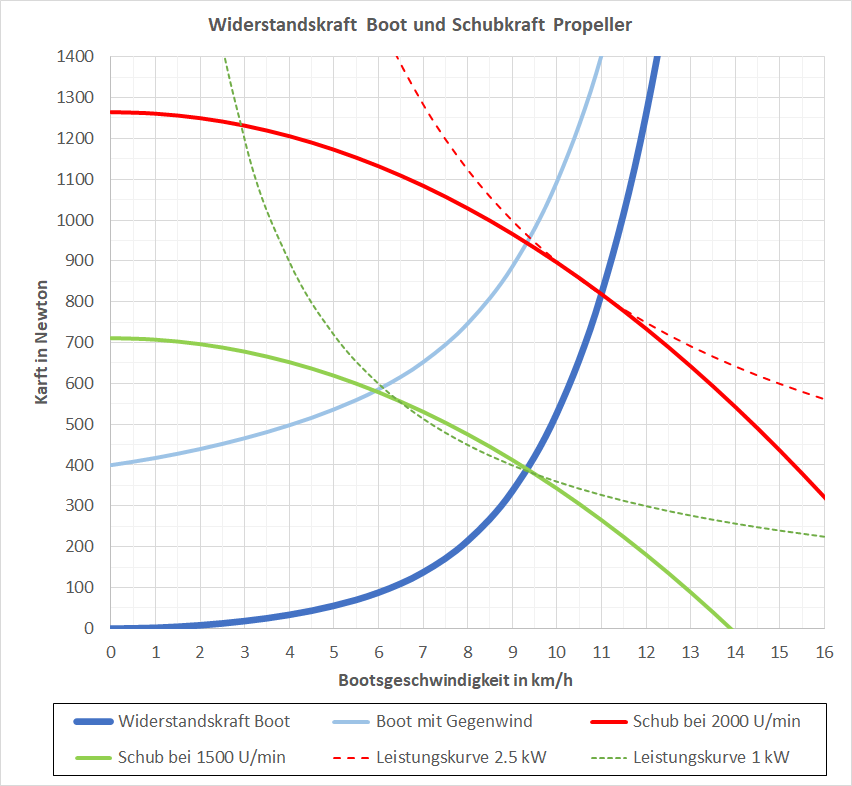
Es sind zwei Kraft-Geschwindigkeit-Kennlinien des Propellerantriebes eingezeichnet, eine rote Kurve für eine Drehzahl von 2000 U/min und eine grüne Kurve für 1500 U/min. Zusätzlich sind gestrichelt noch die entsprechenden Kurven (Hyperbeln) mit konstanter Leistung eingezeichnet. Diese Leistungskurven beziehen sich auf die Leistung im Wasser, sie sind nicht Leistungskurven des Motors.

Im Weiteren sind zwei Kraft-Geschwindigkeit-Kennlinien des Bootes eingezeichnet. Die blaue Kurve für Flaute, die hellblaue Kurve für Gegenwind mit 50 km/h (Windstärke 7), welcher hier auf das stillstehende Boot mit einer Kraft von 400 N wirkt (entspricht der Gewichtskraft von etwa 40 kg). Bei 100 km/h Gegenwind wären es 1600 N.

Das Boot erreicht in der Flaute bei einer Motordrehzahl von 2000 U/min die Rumpfgeschwindigkeit von 11 km/h. Die Schubkraft beträgt 820 N, was eine Antriebsleistung im Wasser von 2.5 kW ergibt (3.05 m/s mal 820 N). Bei einer Drehzahl von 1500 U/min läuft das Boot noch 9.3 km/h. Die erforderliche Schubkraft beträgt 385 N, das ergibt eine Leistung von 1 kW (2.6 m/s mal 385 N). In diesem Beispiel wird für eine 18 % höhere Geschwindigkeit 150 % mehr Leistung benötigt. Mit der gleichen Energiemenge (Diesel oder Batteriekapazität) und gleichem Propellerwirkungsgrad wäre die Reichweite mit 9.3 km/h mehr als doppelt so gross wie mit 11 km/h.

Bei 50 km/h Gegenwind erreicht das Boot bei 2000 U/min noch eine Geschwindigkeit von 9.3 km/h, bei 1500 U/min noch 6 km/h. Wäre die Windgeschwindigkeit 75 km/h (Windstärke 9), ist die Windkraft im Stillstand 900 Newton. Mit 1500 U/min (einem 1.5 kW Motor) käme man in diesem Beispiel nicht gegen an.

Das hier ist nur ein Beispiel für eine kleine Segelyacht mit 4 kW Motor und relativ kleinem Propeller. Für andere Boote gelten andere Werte. Das Grundprinzip des Zusammenhangs zwischen Widerstandskraft Boot gegenüber Schubkraft bei verschiedenen Propellerdrehzahlen bleibt aber erhalten.

Motor

In den meisten Segelyachten ist ein Dieselmotor eingebaut. Bei einem Benzinmotor können sich explosive Dämpfe in der Bilge sammeln, darum ist er in Segelyachten kaum zu finden. Bei Aussenbordern dominiert der Benzinmotor. In Binnenrevieren gibt es einen Trend zu Booten mit Elektromotor.

Eine Leistung von 1 PS entspricht 0.74 kW oder 1 kW = 1.36 PS.

Verbrennungsmotoren

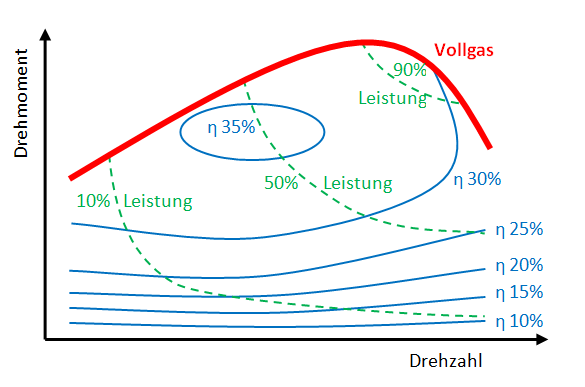
Ein Motor hat seine Nennleistung bei seiner Nenndrehzahl. Beim Verbrennungsmotor ist die Nennleistung die maximal mögliche Abgabeleistung. Er kann seine Nennleistung nur abgeben, wenn auf dem Weg dorthin das Lastmoment immer kleiner als sein Drehmoment ist. Er bleibt auf der Drehzahl stehen, wo sein Drehmoment gleichgross wie das Lastmoment ist. Im Leerlauf (Standgas) hat der Motor keine Abgabeleistung. Sein inneres Drehmoment ist dann gleichgross wie sein inneres Reibungsmoment. Mit dem Gashebel wird die Treibstoffzufuhr vergrössert, was zu einer höheren Drehzahl führt, solange das Lastmoment nicht grösser als das Motormoment ist.

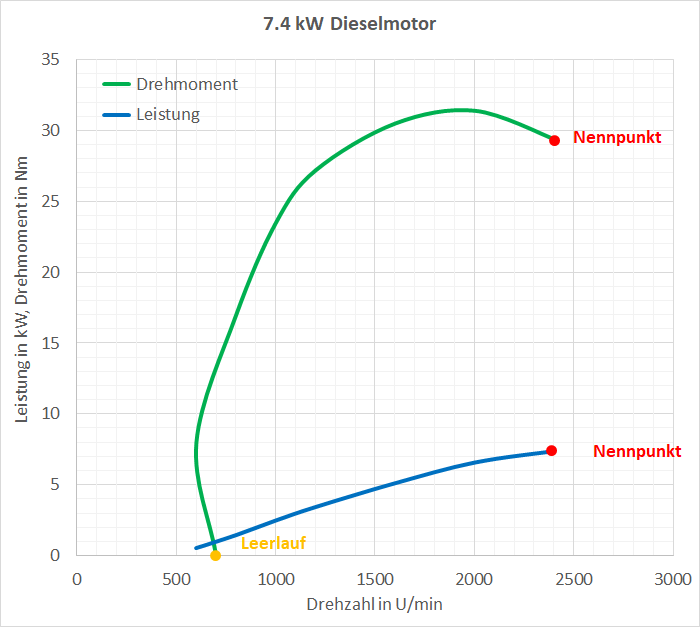
Ein Dieselmotor hat einen breiten Bereich mit hohem Drehmoment als der Benzinmotor. Der Dieselmotor hat eine höhere Verdichtung (höherer Zylinderdruck). Aus diesem Grund muss er massiver gebaut sein. Er hat er einen besseren Wirkungsgrad als der Benzinmotor.

Elektromotoren

Als Bootsmotor werden folgende 3 Typen von Elektromotoren eingesetzt:

• Gleichstrommotor: Die Stromführung in die Wicklungen des Rotors erfolgt über Kontaktflächen (Kommutator), welche vor Korrosion geschützt werden müssen. Im Stator sind Permanentmagnete. Das Regelgerät macht aus der festen Batteriespannung einer veränderbare Gleichstrom-Ausgangsspannung. Gleichstrommotoren werden heute für Leistungen bis 5 kW angeboten. Der Wirkungsgrad liegt bei etwa 80 %.
• Synchronmotor: Die Wicklungen sind im Stator, im Rotor hat es Permanentmagnete. Im Regelgerät wird aus der festen Batteriespannung Drehstrom mit veränderbarer Frequenz erzeugt. Schon kleinere Synchronmotoren können einen Wirkungsgrad von über 90 % erreichen.
• Asynchronmotor: Es hat im Stator und im Rotor Wicklungen, im Rotor sind sie kurzgeschlossen. Das Regelgerät ist das Gleiche wie für die Synchronmaschine. Der Asynchronmotor kann bis über die doppelte Nenndrehzahl die Nennleistung abgeben. Kleine Asynchronmotoren haben einen schlechteren Wirkungsgrad als die Synchronmotoren.

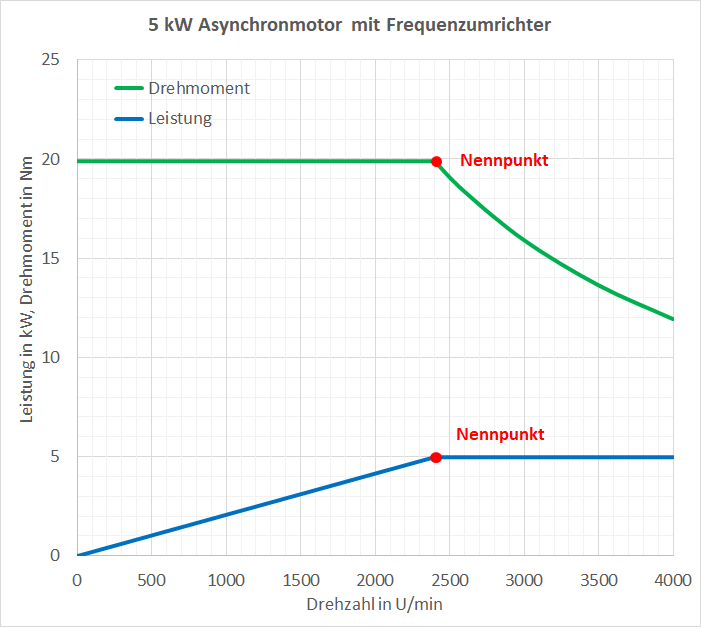
Elektromotoren können im Gegensatz zur Verbrennungsmotoren eine höhere Leistung als die Nennleistung abgeben, wenn es das Regelgerät zulässt. Wenn das aber zulange dauert, überhitzt sich der Motor. Der Motor darf aber dauernd mit seiner Nennleistung belastet werden.

Durch die geringe Drehmoment-Belastung des Propellers bei tiefen Drehzahlen haben Elektromotoren in Booten über den ganzen Betriebsbereich einen guten Wirkungsgrad.

Energieversorgung

Eine Lithiumbatterie mit einem Energieinhalt von 10 kWh ist 100 kg schwer. Ein 3 kW Elektromotor mit 90 % Wirkungsgrad läuft damit 3 Stunden. Bei 10 km/h gibt das eine Strecke von 30 km, die in einem Binnenrevier oft reicht. Ein grösseres Boot benötigt aber mehr Leistung und somit auch eine grössere Batterie für die gleiche Strecke.

Ein Liter Dieselöl hat einen Energieinhalt von 10 kWh und wiegt 0.84 kg. Bei einem Motorenwirkungsgrad von 30 % benötigt der Diesel für 3 kW Motorleistung 1 Liter Dieselöl (0.84 kg Gewicht) pro Stunde. 100 kg Dieselöl (120 Liter) reichen für 120 Stunden Fahrt mit 3 kW. In Bezug auf die Reichweite ist ein Dieselmotor einem Elektromotor weit überlegen (Faktor 40).

Propellergrössen

Die beiden wesentlichen Grössen eines Bootspropellers sind sein Durchmesser und seine Steigung. Darüber hinaus gibt es noch weitere Parameter wie Flügelzahl, Nabendurchmesser, Flächenverhältnis, Flügelhang, Flügelrücklage und die Profilform, die hier nicht behandelt werden.

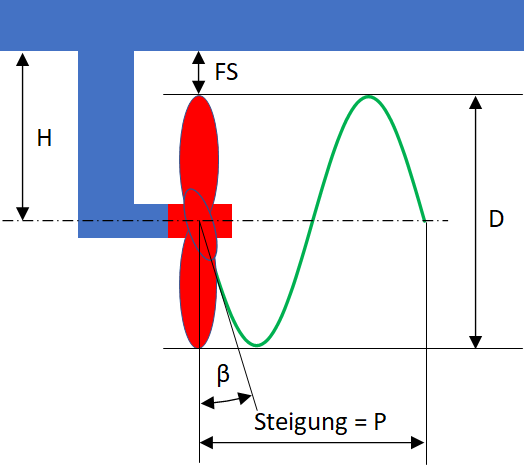
Bei Propellern werden Durchmesser D und Steigung P meistens in Zoll angegeben. Die Steigung ist die Strecke, welche der Propeller in einer gedachten weichen Masse bei einer Umdrehung zurücklegen würde.

\(P = D \cdot \pi \cdot \tan{\beta}\)

\(P\) = Propellersteigung in Zoll (P steht für Pitch, englisch für Steigung)
\(D\) = Propellerdurchmesser in Zoll
\(\beta\) = Steigungswinkel, gemessen bei 70 % des Radius

Beispiel: Bei einem Propellerdurchmesser von 10 Zoll und einem Steigungswinkel von 20 ° beträgt die Propellersteigung 10 Zoll.

Bei üblichen Propellern liegt die Propellersteigung im Bereich von 50 bis 150 % des Propellerdurchmessers, oft liegen die Werte nahe zusammen. Die erste Zahl der Typenbezeichnung bezieht sich auf den Propellerdurchmesser, die zweite auf die Propellersteigung. Der Buchstabe LH steht für linksdrehend (Gegenuhrzeigersinn) vom Heck aus gesehen, RH für rechtsdrehend. Die meisten Bootsdiesel sind linksdrehend. Eine weitere Grösse bezieht sich auf die Norm für den Wellenanschluss. Beispiel für die Bezeichnung: 11 LH 8, Konus USA 1"

Je grösser der Propellerdurchmesser ist, desto mehr Wasser wird pro Umdrehung bewegt, desto mehr Schub wird erzeugt und desto besser wird der Propellerwirkungsgrad. Bei Segelbooten bewirkt ein grosser Propellerdurchmesser auch mehr Widerstand beim Segeln, darum werden häufig Klapp-Propeller verwendet. Der maximale Propellerdurchmesser ist durch die Einbausituation begrenzt. Die massgebende Grösse ist der Freischlag, der Abstand zwischen Propeller und Bootskörper. Dieser Freischlag (FS) sollte mehr als 20 % des Propellerdurchmessers betragen, um Vibrationen zu vermeiden. Das gibt einen maximalen Propellerdurchmesser (D) von 1.4 mal Abstand Propellerachse zu Bootskörper (H).

\(FS > 0.2 \cdot D\)
\(D < 1.4 \cdot H\)

\(FS\) = Freischlag in Zoll (Abstand Propeller zu Bootskörper)
\(D\) = Propellerdurchmesser in Zoll
\(H\) = Abstand Propellerachse zu Bootskörper in Zoll

Beispiel: Bei einem Abstand (H) von 8 Zoll (20 cm) sollte der Propellerdurchmesser (D) nicht grösser als 11 Zoll sein.

Propellerauswahl

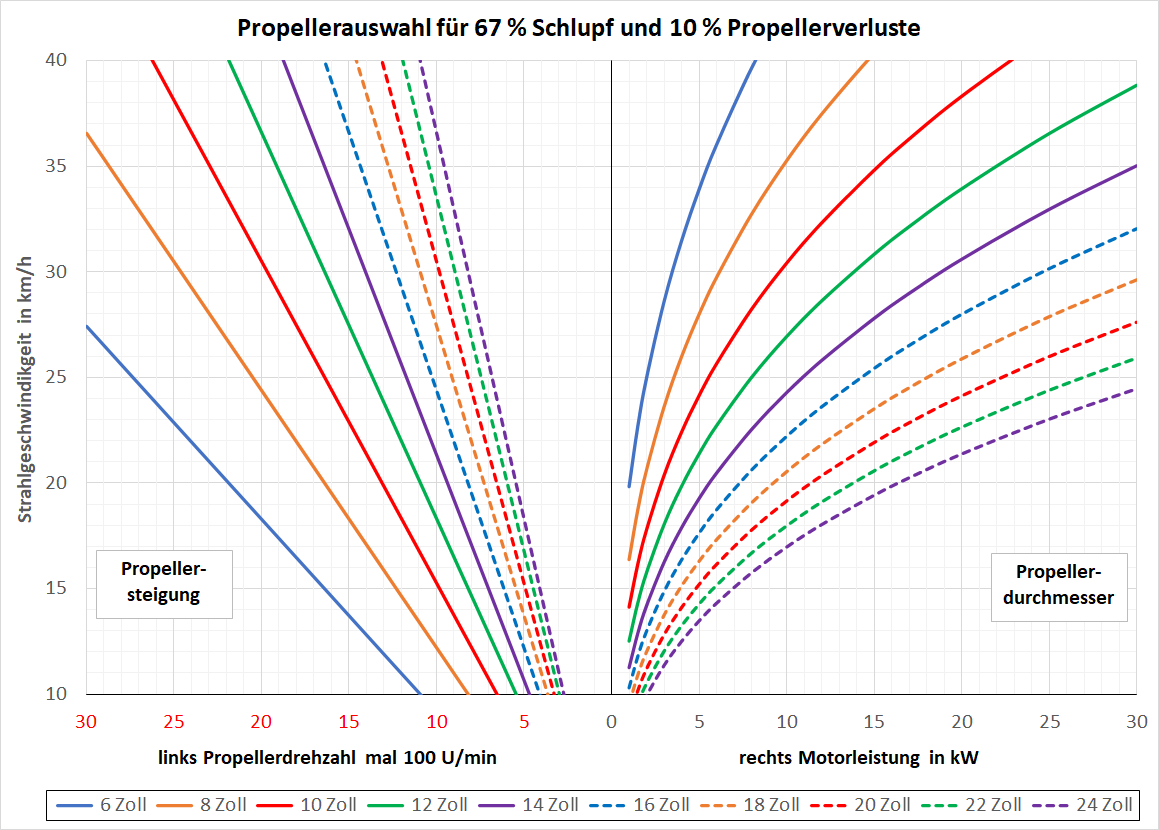
Mit der gewünschten Geschwindigkeit und Motorleistung, kann man mit den beiden untenstehenden Diagrammen den Propellerdurchmesser und die Propellersteigung bestimmen:

• Propellerauswahl für 67 % Schlupf. Die Motorleistung bezieht sich auch eine Bootsgeschwindigkeit von 33 % der Strahlgeschwindigkeit (67 % Schlupf). Bei dieser Auslegung wird der Motor bei Vollgas aus dem Stillstand, einer Belastung durch Gegenwind oder geschleppte Boote nicht überlastet. Im Betriebspunkt bei geringerem Schlupf nimmt er weniger als die Nennleistung auf.
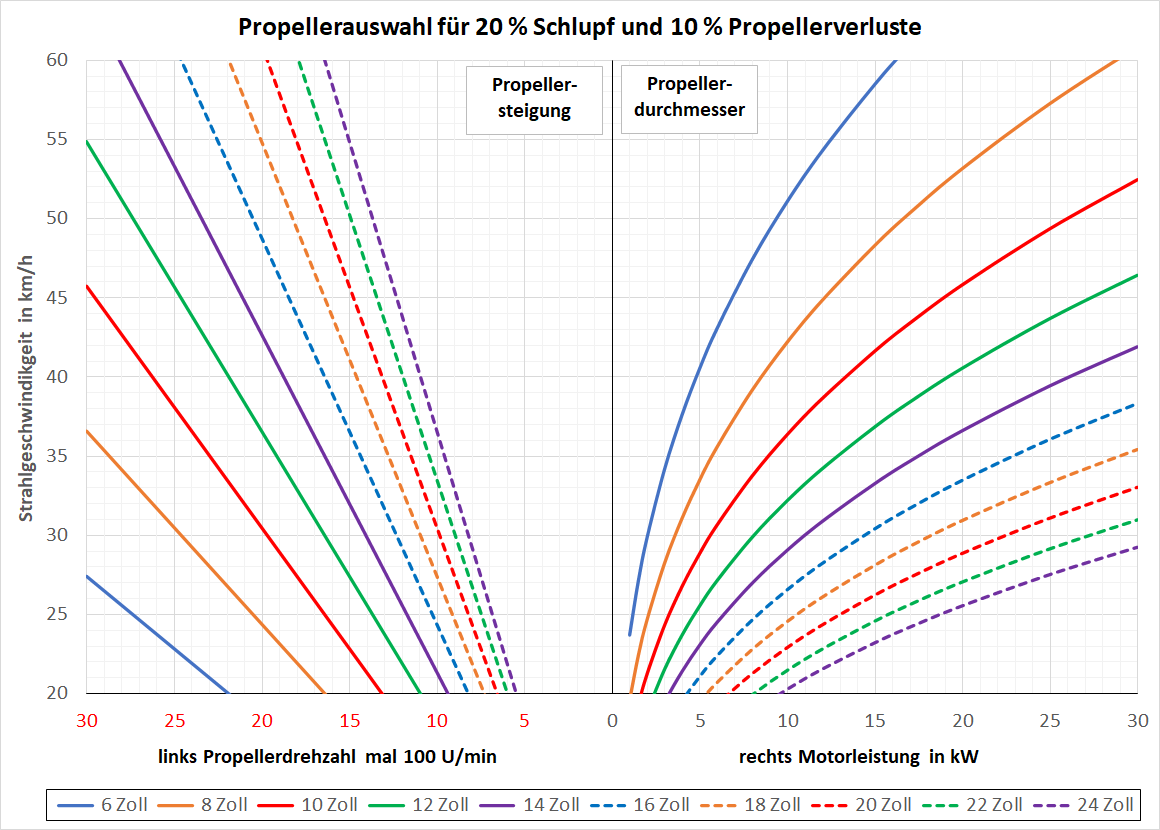
• Propellerauswahl für 20 % Schlupf. Die Motorleistung bezieht sich auch eine Bootsgeschwindigkeit von 80 % der Strahlgeschwindigkeit (20 % Schlupf). Bei dieser Auslegung wird die Drehzahl des Motors kontinuierlich der Bootsgeschwindigkeit angepasst, damit der Schlupf nicht zu gross wird und der Motor nicht überlastet wird. Dieses Diagramm ist für schnelle Boote geeignet.

In den Diagrammen kann auf der rechten Seite die Motorleistung, der Propellerdurchmesser und die Strahlgeschwindigkeit abgeschätzt werden. Auf der linken Seite bei gleicher Strahlgeschwindigkeit die Propellerdrehzahl und die Propellersteigung. Das funktioniert auch umgekehrt oder über die Wahl der Strahlgeschwindigkeit (110 bis 200 % der gewünschten Bootsgeschwindigkeit). Grundlage für das Diagramm ist die Strahltheorie und hier angenommene 10 % Verlustleistung durch die Reibung am Propeller, welche zur Motorenleistung dazu gerechnet wird.

Die Propellerauswahl führt zu 3 verschiedenen Ergebnissen für den Betrieb im Nennpunkt des Motors (Nennleistung und Nenndrehzahl):

1. Der Propeller passt. Der Antriebsmotor kann seine Nennleistung abgeben und wird nicht überlastet.
2. Der Propeller ist zu schwach. Der Antriebsmotor kann seine Nennleistung nicht abgeben, da er bei seiner Nenndrehzahl vom Propeller zu wenig belastet wird.
3. Der Propeller ist zu stark. Der Antriebsmotor erreicht seine Nenndrehzahl nicht, da er vom Propeller zu stark belastet wird. Der Motor erreicht somit seine Nennleistung nicht, er kann überlastet werden.

2 Schlussfolgerungen zur Propellerwahl:

• Es ist vorteilhaft, den grösstmöglichen Propellerdurchmesser zu wählen.
• Dass der Propeller genau passt, ist Zufall. Motoren, Getriebe und Propeller gibt es in festen Abstufungen, man muss Kompromisse machen.

Beispiel für eine Propellerauswahl

Die ausgewählte Segelyacht hat eine Wasserlinienlänge von 6 m (11 km/h Rumpfgeschwindigkeit) und einen etwas überdimensionierten Motor mit 5 kW Nennleistung bei einer Nenndrehzahl von 2400 U/min. Der maximal mögliche Propellerdurchmesser ist 11 Zoll. Somit ist ein Schlupf im Bereich von 20 % nicht möglich.

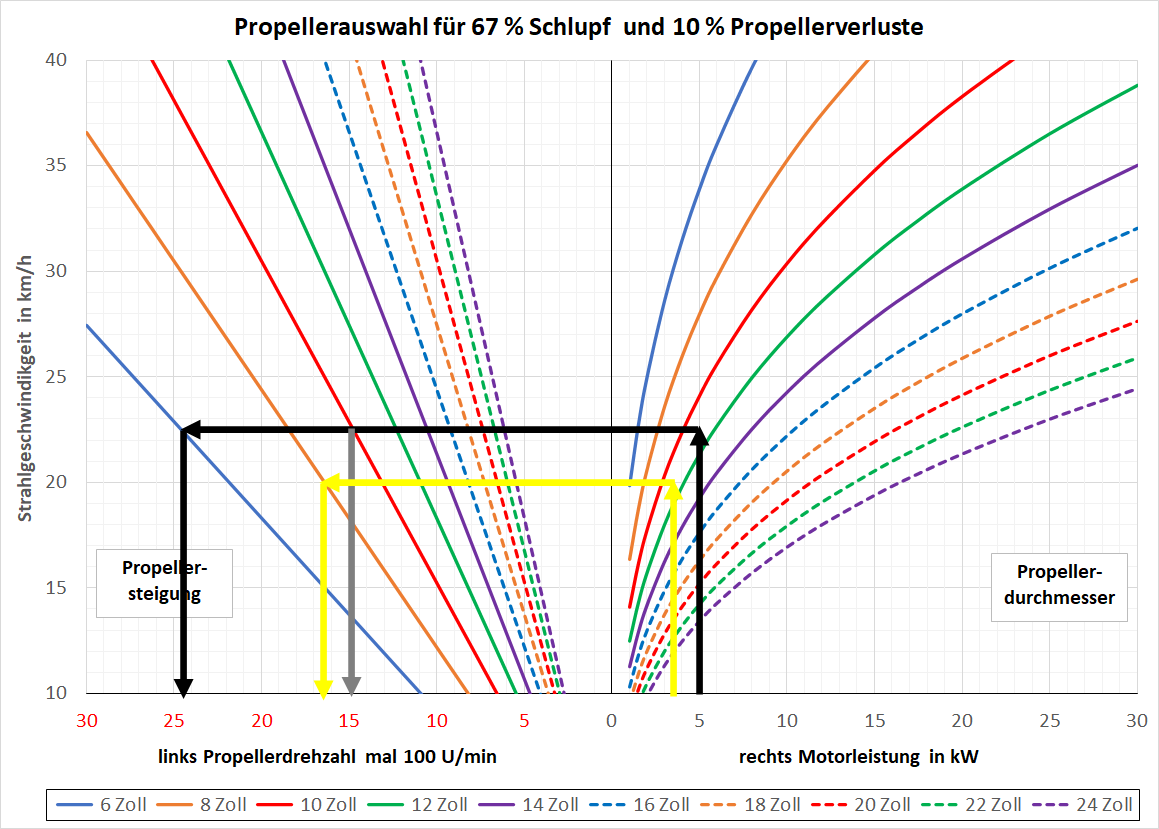
Aus dem obenstehenden Diagramms können folgende Schlussfolgerungen gezogen werden:

1. Ausgehend von 5 kW Motorleistung und einem maximalen Propellerdurchmessers von 11 Zoll ergibt sich eine Strahlgeschwindigkeit von 22.5 km/h. Bei dieser Strahlgeschwindigkeit und einer Propellersteigung von 6 Zoll zeigt das Diagramm einer Propellerdrehzahl von 2450 U/min. Dieser Weg ist mit den schwarzen Pfeilen eingezeichnet.
2. Ausgehend von einer Rumpfgeschwindigkeit von 11 km/h errechnet sich aus der Stahlgeschwindigkeit von 22.5 km/h ein Schlupf von etwa 50 %. Bei dem ist noch ein Propellerwirkungsgrad von 60 % zu erwarten. Bei einem kleineren Propellerdurchmesser würde die Strahlgeschwindigkeit und somit der Schlupf grösser werden, der Wirkungsgrad würde sich verschlechtern.
3. Der Motor hat 5 kW Leistungsabgabe bei 2400 U/min, was etwa zu den 2450 U/min passt. Propeller mit 11 Zoll Durchmesser und 6 Zoll Steigung sind aber nicht im Standardprogramm der Hersteller. Die geringste Steigung für einen Durchmesser von 11 Zoll beträgt 8 Zoll.
4. Um die volle Leistung abzugeben, wird ein Untersetzungsgetriebe benötigt. Wenn schon ein Getriebe erforderlich ist, kann auch gleich eine noch höhere Propellersteigung gewählt werden. In diesem Beispiel (grauer Pfeil) 10 Zoll, was eine Propellerdrehzahl von 1480 U/min ergibt. Das Getriebe hat eine Untersetzung von 2400 auf 1480 U/min (1.62). Der Getriebewirkungsgrad von 97 % verschlechtert den Gesamtwirkungsgrad um 3 %. Durch die geringere Propellerdrehzahl gibt es aber weniger Reibungsverluste am Propeller, was die Reibungsverluste im Getriebe in etwa wieder ausgleicht.
5. Eine Alternative (gelbe Pfeile) ist bei einem Propellerdurchmesser von 11 Zoll und einer Propellersteigung von 8 Zoll eine geringere Motorleistung anzunehmen. Die Motorleistung ist proportional zur Motordrehzahl und erreicht das Maximum bei der Nenndrehzahl. Der Motor hat bei 2400 U/min eine Leistung von 5 kW, bei 1640 U/min hat er noch 3.4 kW. Die Strahlgeschwindigkeit reduziert sich auf  20 km/h, was noch einen Schlupf von 45 % ergibt und einen Propellerwirkungsgrad um die 64 % erwarten lässt. Damit der Motor nicht überlastet wird, ist seine Drehzahl auf 1640 U/min zu begrenzen.

Strahltheorie

Bei der Strahltheorie geht man von einem zylindrischen Wasserstrahl aus, welcher durch einen idealen Propeller nach hinten bewegt wird. Reibungsverluste am Propeller und im Wasser (Wirbel) werden dabei nicht berücksichtigt.

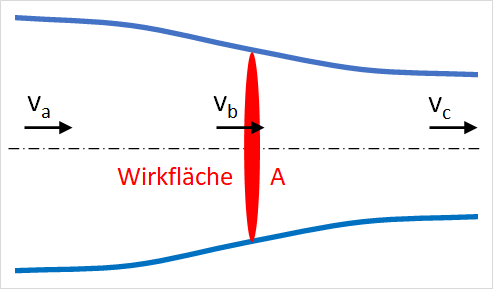
\(v_a\) = Strahlgeschwindigkeit vor dem Propeller in m/s (entspricht der Bootsgeschwindigkeit)
\(v_b\) = Strahlgeschwindigkeit beim Propeller in m/s (ist der Mittelwert von \(v_c\) und \(v_a\))
\(v_c\) = Strahlgeschwindigkeit nach dem Propeller in m/s (Steigung mal Drehzahl)

Aus der Strahltheorie ergeben sich folgende Beziehungen:

\(\dot{m} = \rho \cdot A \cdot v_b\)
\(F = \dot{m}  \cdot (v_c - v_a)\)
\(P_B = F \cdot v_a\)
\(P_M = F \cdot v_b\)

\(\eta = \dfrac{P_B}{P_M}\)

\(s = \dfrac{v_c - v_a}{v_c}\)

\(v_c = n \cdot p\)
\(v_a = v_c \cdot (1 - s)\)
\(v_b = v_c \cdot (1 - \frac{s}{2})\)

\(A = \pi \cdot (\frac{d}{2})^2\)

\(\dot{m}\) = Massenstrom des Strahls in kg/s
\(\rho\) = Spezifisches Gewicht des Wassers = 1000 kg/m³ (Meerwasser 1005 kg/m³)
\(A\) = Querschnittsfläche des Propellers in m²
\(F\) = Schubkraft des Propellers in N (Newton)
\(P_B\) = Abgabeleistung des Propellers ans Boot in Watt
\(P_M\) = Aufnahmeleistung des Propellers vom Motor in Watt (hier ohne Reibungsverluste)
\(\eta\) = Wirkungsgrad (dimensionslos)

\(s\) = Schlupf (dimensionslos)
\(n\) = Propellerdrehzahl in U/s  (30 U/s = 1500 U/min)
\(p\) = Propellersteigung in m/U
\(d\) = Durchmesser des Propellers in m

Umgerechnet auf den Schlupf entstehen folgende Gleichungen:

\(\dot{m} = \rho \cdot A \cdot v_c \cdot (1 - \frac{s}{2}) \sim d^2 \cdot n \cdot p\)
\(F = \rho \cdot A \cdot v_c^2 \cdot (s - \frac{s^2}{2}) \sim d^2 \cdot n^2 \cdot p^2\)
\(P_B = \rho \cdot A \cdot v_c^3 \cdot (s - \frac{3 \cdot s^2}{2} + \frac{s^3}{2}) \sim d^2 \cdot n^3 \cdot p^3\)
\(P_M = \rho \cdot A \cdot v_c^3 \cdot (s - s^2 + \frac{s^3}{4}) \sim d^2 \cdot n^3 \cdot p^3\)
\(\eta = \dfrac{1- s}{1 - \frac{s}{2}}\)

In üblichen Herleitungen wird die Propellersteigung im Verhältnis zum Propellerdurchmesser angegeben. Dadurch bekommt der Propellerdurchmesser mehr Gewicht (4. und 5. Potenz). Die Steigung ist dann im Freifahrdiagramm konkreter Propeller enthalten.

Verwendete Quellen:

• Segeltheorie und Praxis, C.A. Marchaj, Ausgabe 1971, ISBN 3-7688-0108-X
• Motorkreuzer und schnelle Sportboote, Juan Baader, 1972
• Konzeptentwicklung für den Entwurf von Schiffspropellern, Diplomarbeit Sören Jörke, 2017