Auf einen elektrischen Leiter (oder ein Wicklungsstrang) im Magnetfeld wirkt eine Kraft (Lorenzkraft), welche proportional zum Leiterstrom, der Anzahl Windungen zur Leiterlänge im Luftspalt und zur Induktion (magnetische Flussdichte) ist.
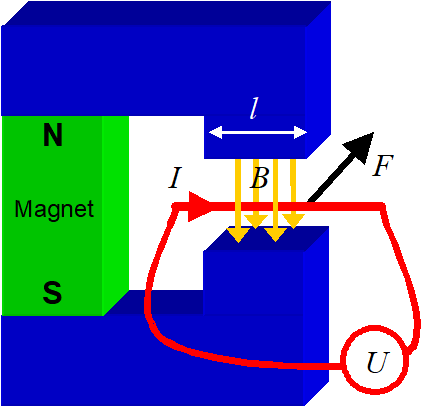
\(F = I \cdot B \cdot l \cdot w\) = Grundbeziehung für die Lorentzkraft
\(F\) [N] = Kraft auf Leiter gegenüber dem Magnetfeld
\(I\) [A] = Leiterstrom
\(B\) [T] = Induktion = Magnetische Flussdichte
\(l\) [m] = Leiterlänge im Luftspalt
\(w\) [-] = Anzahl Windungen
Wenn sich der Leiter bewegt, wird eine Spannung induziert, deren Stärke proportional zur Induktion, zur Geschwindigkeit, zur Leiterlänge und zur Windungszahl ist. Diese Spannung nennt man auch EMK (Elektromotorische Kraft).
\(U_i = v \cdot B \cdot l \cdot w\) = Induzierte Spannung im bewegten Leiter
\(U_i\) [V] = Induzierte Spannung (EMK)
\(v\) [m/s] = Leitergeschwindigkeit gegenüber dem Magnetfeld
Wenn ein Strom fliesst, wirkt zusätzlich der ohmsche Spannungsabfall über den Widerstand des Leiters. Die im Widerstand anfallende Verlustwärme ist auch die Differenz zwischen der mechanischen und elektrischen Leistung.
\(U = U_i + R \cdot I\) = Beziehung zur einer Spannungsquelle
\(U\) [V] = Spannung
\(R\) [Ω] = Ohmischer Leiterwiderstand
\(P_m = F \cdot v\) [W] = Mechanische Leistung
\(P_e = U \cdot I\) [W] = Elektrische Leistung
\(|P_m - P_e| = R \cdot I^2\) [W] = Verlustleistung
Aus dieser einfachen Beziehung ist zu erkennen, dass die Verluste quadratisch mit der abgenommenen Kraft zunehmen, weil die Kraft proportional zum Strom ist. Es ist auch zu erkennen, dass die Verluste unabhängig von der Geschwindigkeit sind. Bei einem Motor wird über den Luftspaltradius aus der Kraft ein Drehmoment und aus der Geschwindigkeit eine Drehzahl.
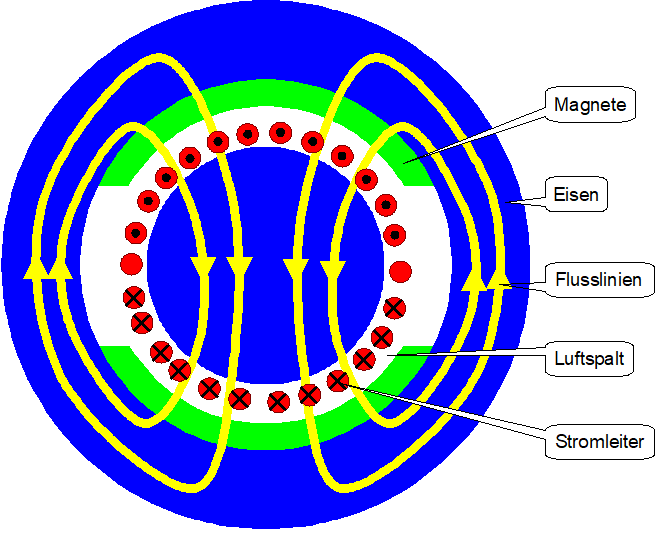
Die Anzahl Windungen hat mit der Kraftwirkung direkt nichts zu tun, sondern ist nur eine Impedanzanpassung an die elektrische Quelle. Eine hohe Windungszahl ergibt eine hohe Spannung und einen geringen Strom.
Der maximale Strom ist die mögliche Leiterquerschnittsfläche \(A_{Cu}\) [m²] (Luftspaltdicke mal Magnetbreite) mal die zulässige Stromdichte \(J\) [A/m²] (z.B. 10 MA/m²). Je nach Wicklungsart (Hohlräume) und Dicke der Drahtisolation ist die Summe der Ströme etwa konstant. Die Kraft (das Drehmeoment) ist also unabhängig von der Anzahl Windungen, sie hängt von der zulässigen Stromdichte und dem Füllfaktor ab.
Die Kupferwärmeverluste betragen \(P_{v_{{Cu}}}=R \cdot I^2\) [W]. Bei einer Wicklung mit \(w\) Windungen nimmt der Leiterquerschnitt mit \(A_{Cu}/w\) ab und die Wicklungslänge mit \(l \cdot w\) zu. Der Widerstand \(R=\rho \cdot l /A_{Cu}\) nimmt also mit der Windungszahl quadratisch zu. \(\rho\) von Kupfer ist 17 nΩm.
Der Strom nimmt mit \(I/w\) ab, was von der Wicklungszahl unabhängige Kupferwärmeverluste \(R \cdot w^2 \cdot (I/w)^2=R \cdot I^2\) ergibt. Überschlagsmässig (mit Füllfaktor 1) sind die Kupferverluste \(P_{v_{{Cu}}}=\rho \cdot J^2 \cdot V\). Beim Luftspaltvolumen \(V\) [m³] ist der erforderliche Abstand für die ungehinderte Leiterbewegung zu berücksichigen. In elektrischen Antrieben wird mit dem zulässigen Ankerstrombelägen gerechnet.


