1. Hauptsatz

Jedes System besitzt eine extensive Zustandsgrösse Energie. Sie ist in einem abgeschlossenen System konstant. In einem abgeschlossenen System ist die Summe aller Veränderungen der Energie Null (zugeführte Energie wird positiv und abgeführte Energie wird negativ gezählt).

2. Hauptsatz

Alle natürlichen Prozesse sind irreversibel. Wärme kann nie von selbst von einem Körper niedriger auf einen Körper hoher Temperatur übergehen.

3. Hauptsatz

Die minimale Temperatur ist 0 K (- 273,15 °C).

Carnotfaktor, Energie gleich Exergie und Anergie

Energie kann nicht produziert oder vernichtet werden (1. Hauptsatz der Thermodynamik).

Energien haben aber eine unterschiedliche Wertigkeit, je höher die Temperatur, desto wertvoller ist die Energie. Wenn die Umgebungstemperatur zum Beispiel 20 °C beträgt, dann ist ein Energiespeicher mit 20 Liter Wasser auf einem Temperaturniveau von 40 °C weniger wert, als einer mit 10 Liter Wasser auf 60 °C, wobei beide den gleichen Energieinhalt von 1672 kJ (Wärmekapazität mal Temperaturdifferenz) gegenüber der Umgebungstemperatur von 20 °C haben. Wenn man in den Speicher mit 10 Liter auf 60 °C weitere beliebig vorhandene 10 Liter aus 20 °C Umgebungstemperatur hinzufügt, erhält man 20 Liter mit 40 °C. Diese Vermischung lässt sich ohne zusätzliche Energie nicht rückgängig machen (2. Hauptsatz der Thermodynamik).

Grundlage für die Bewertung ist der Energie auf verschiedenen Temperaturen ist der theoretisch maximale thermische Wirkungsgrad von Wärmekraftmaschinen, der Carnotfaktor. Dieser errechnet sich aus der Differenz der höchsten zur tiefsten Temperatur durch die höchste Temperatur in Kelvin (0 °C = 273,15 K) welche in einem Prozess vorkommen. Die theoretisch maximal gewinnbare mechanische Energie aus einer Temperaturdifferenzen wird mit dem Carnotfaktor beschrieben. In der Gleichung müssen die Temperaturen als Absolutwerte in Kelvin verwendet werden.  \[\eta_{\text{Carnot}}=\frac{T_{\text{hoch}}-T_{\text{tief}}}{T_{\text{hoch}}}\]

Um die aus Wärme theoretisch gewinnbare mechanische Energie zu quantifizieren, gibt es die Begriffe Exergie und Anergie:

  1. Die Exergie ist die Energie, welche theoretisch in mechanische Energie umgewandelt werden kann.
  2. Die Anergie ist die Energie minus deren Exergie, also nur noch Wärme auf dem Niveau der Umgebungswärme.
  3. Die Energie ist die Summe aus Exergie und Anergie

Beispiel

Zwei unterschiedlich warme Wasserbehälter werden zusammen geschüttet.

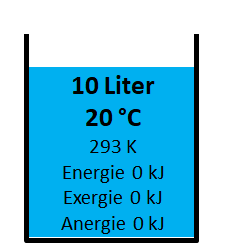
Wenn 10 Liter Wassermenge mit 20 °C und 10 Liter mit 60 °C zusammengeleert werden, ergibt sich 20 Liter mit 40 °C. Die Energie bleibt erhalten, ohne zusätzliche Energie kann dieser Vorgang aber nicht mehr rückgängig gemacht werden.

Kalter Wasserbehälter

Im 10 Liter Behälter mit 20 °C besteht keine Differenz zur Umgebungstemperatur, aus diesem Grund hat er keinen Energieinhalt. Energie, Exergie und Anergie ist 0 kJ.

\(Energie=m \cdot c_{\text{p}} \cdot (T_{\text{Medium}}-T_{\text{Umgebung}}) \) = 10 kg 4.18 kJ/kgK (293 K - 293 K) = 0 kJ

\(\eta_{\text{Carnot}}=\frac{T_{\text{Medium}}-T_{\text{Umgebung}}}{T_{\text{Medium}}}\) = (293 K - 293 K) / 293 K = 0 = 0 %

\(Exergie=\eta_{\text{Carnot}} \cdot Energie\) = 0 0 kJ = 0 kJ

\(Anergie=Energie - Exergie\) = 0 kJ - 0 kJ = 0 kJ

Im kalten Wasserbehälter steckt keine Energie da er die gleiche Temperatur wie die Umgebung hat.

Heisser Wasserbehälter

Im 10 Liter Behälter mit 60 °C (333 K) besteht eine Differenz zur Umgebungstemperatur, aus diesem Grund hat er einen Energieinhalt.

\(Energie=m \cdot c_{\text{p}} \cdot (T_{\text{Medium}}-T_{\text{Umgebung}}) \) = 10 kg 4.18 kJ/kgK (333 K - 293 K) = 1672 kJ

\(\eta_{\text{Carnot}}=\frac{T_{\text{Medium}}-T_{\text{Umgebung}}}{T_{\text{Medium}}}\) = (333 K - 293 K) / 333 K = 0.12 = 12 %

\(Exergie=\eta_{\text{Carnot}} \cdot Energie\) = 0.12  1672 kJ = 200 kJ

\(Anergie=Energie - Exergie\) = 1672 kJ - 200 kJ = 1472 kJ

Im heissen Wasserbehälter stecken 1672 kJ (0.46 kWh) Wärmeenergie gegenüber der Umgebungstemperatur von 20 °C.

Warmer Wasserbehälter

Im zusammengeschütteten 20 Liter Behälter mit 40 °C (313 K) besteht eine Differenz zur Umgebungstemperatur, aus diesem Grund hat er einen Energieinhalt.

\(Energie=m \cdot c_{\text{p}} \cdot (T_{\text{Medium}}-T_{\text{Umgebung}}) \) = 20 kg 4.18 kJ/kgK (313 K - 293 K) = 1672 kJ

\(\eta_{\text{Carnot}}=\frac{T_{\text{Medium}}-T_{\text{Umgebung}}}{T_{\text{Medium}}}\) = (313 K - 293 K) / 313 K = 0.064 = 6 %

\(Exergie=\eta_{\text{Carnot}} \cdot Energie\) = 0.064  1672 kJ = 107 kJ

\(Anergie=Energie - Exergie\) = 1672 kJ - 107 kJ = 1565 kJ

Im warmen 20 Liter Wasserbehälter stecken 1672 kJ Wärmeenergie gegenüber der Umgebungstemperatur von 20 °C, gleichviel wie im heissen 10 Liter Behälter. Gegenüber diesem ist aber die Exergie um 94 kJ geringer.

Zusammenfassung

Durch das Zusammenschütten hat man keine Energie verloren, aber die Arbeitsmöglichkeit aus der Temperaturdifferenz zur Umgebung hat abgenommen. Bei diesem Beispiel hätte man theoretisch 200 kJ mechanische oder elektrische Energie gewinnen können, mit realen Anlagen (zum Beispiel OCR-Prozess oder Peltierelement) wegen dem kleinen Temperaturunterschied vielleicht 10 kJ. Der Vorgang ist ohne zusätzlichen Energieaufwand irreversibel. Mit einer Wärmepumpe oder einem Peltierelement kann man aus den 40 °C warmen Behälter wieder in einen kalten mit 20 °C und einen warmen mit über 60 °C auftrennen. Über 60 ° C, weil die erforderliche mechanische oder elektrische Energie zusätzliche Wärmeenergie ergibt.

Mechanische und elektrische Energie ist reine Exergie.

Die gleichen Gesetzmässigkeiten gelten auch für Temperaturen unter der Umgebungstemperatur.