Der Transformator gehört zu den elektrischen Maschinen. Basis für das Verständnis des Transformators ist die Induktion. Der Transformator ist zu vergleichen mit einem Getriebe, welches hohe Drehzahlen (Spannungen) in tiefe transformiert und dort dafür grössere Drehmomente (Ströme) hat.
Vereinfacht interessiert die Leistung und das Übersetzungsverhältnis. Ohne Berücksichtigung der Verluste, der Streuung und der Magnetisierung ergeben sich folgende Beziehungen, welche auf grosse Transformatoren gut zutreffen:
| Grösse | Einheit | Beziehung | Bezeichnung |
|---|---|---|---|
| N1 | - | Anzahl Primärwindungen | |
| N2 | - | Anzahl Sekundärwindungen | |
| ü | - | ü = N1 / N2 | Übersetzungsverhältnis |
| U1 | V | Primärspannung | |
| I1 | A | Primärstrom | |
| S1 | VA | S1=U1 I1 | Primärleistung (einphasig) |
| U2 | U | U2 = U1 / ü | Sekundärspannung |
| I2 | I | I2 = I1 ü | Sekundärstrom |
| S2 | VA | S2 = S1 | Nennleistung (ohne Verluste) |
Die Dimensionierung und Messung von Transformatoren hat viele Ähnlichkeiten mit dem Vorgehen bei elektrischen Maschinen, vor allem der Asynchronmaschinen.

Grössengesetze beim Transformator
Die übertragbare Leistung eines Transformators ist bei gegebener Flussdichte und Stromdichte proportional zur Eisenquerschnittsfläche und Kupferquerschnittsfläche. Die Verluste eines Transformators bei gegebenen spezifischen Eisenverlusten und Stromdichten sind proportional zum Eisen- und Kupfervolumen.
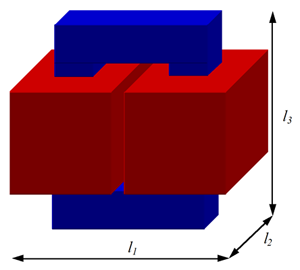
Abmessungen eines Transformators.
|
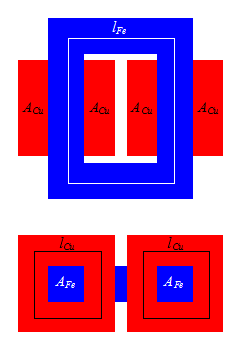
Flächen eines Transformators
|
Für geometrisch ähnliche Transformatoren mit der Länge l [m] ergeben sich folgende Grössengesetze:
| Grösse | Beziehung | Vereinfachung | Konsequenzen |
|---|---|---|---|
| Übertragungsleistung | S = U I ~ AFe B ACu SStromdichte | S ~ l 4 | Die Übertragungsleistung steigt mit der 4. Potenz der Abmessung |
| Transformatorverluste | Pv ~ mCu Pv'Cu + mFe Pv'Fe | Pv ~ l 3 | Die Verluste sind proportional zum Volumen. |
| Transformatorvolumen | V ~ l1 l2 l3 | V ~ l 3 | Je grösser ein Transformator ist, desto besser wird sein Wirkungsgrad (bis 99,8%) |
| Transformatoroberfläche | A ~ 2 (l1 l2 + l1 l3 + l2 l3) | A ~ l 2 | Je grösser ein Transformator ist, desto mehr Probleme hat er mit der Abführung der Verlustwärme |
Zusammenfassung: Je grösser ein Transformator ist, desto besser ist sein Wirkungsgrad und desto besser muss er gekühlt werden.
Ersatzschaltbild und Nenngrössen
Das Ersatzschaltbild eines Transformators kann die galvanische Trennung zwischen Primär- und Sekundärseite nicht darstellen. Die Transformation kann ebenfalls nicht dargestellt werden. Aus diesem Grund werden auf der Sekundärseite gestrichene (mit Apostroph versehene) Grössen eingesetzt.
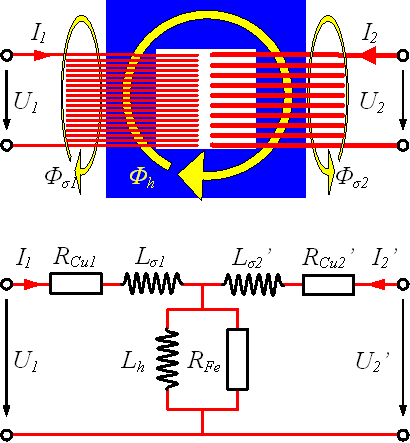
Spannung primär \(U_1\) [V]
Strom primär \(I_1\) [A]
Kupferwiderstand der Wicklung primär \(R_\text{Cu1}\) [Ω]
Streuinduktivität primär \(L_\text{σ1}\) [H]
Streufluss primär \(Φ_\text{σ1}\) [Vs]
Hauptinduktivität \(L_h\) [H]
Hauptfluss durch beide Windungen \(Φ_h\) [Vs]
Ersatzwiderstand für die Eisenverluste \(R_\text{Fe}\) [Ω]
Streuinduktivität sekundär \(L_\text{σ2}\) [H]
Streufluss sekundär \(Φ_\text{σ2}\) [Vs]
Kupferwiderstand der Wicklung sekundär \(R_\text{Cu2}\) [Ω]
Strom sekundär \(I_2\) [A]
Spannung sekundär \(U_2\) [V]
Je grösser der Streufluss ist, desto weicher ist der Transformator. Das bedeutet, dass die Ausgangsspannung mit zunehmender sekundärer Belastung stärker abnimmt, als bei einem harten Transformator mit geringer Streuung. Der Vorteil eines weichen Transformators ist ein geringer Kurzschlussstrom. Die Streuung ergibt sich aus der Konstruktion der Windungen.
Ein Transformator hat auch schon ohne sekundäre Last eine Stromaufnahme in der Primärwicklung (Leerlaufstrom). Die wird für die Magnetisierung des Eisens benötigt. Da das Eisen gut ausgenützt wird, ist es nahe an der Sättigung magnetisiert. Eine Erhöhung der Primärspannung würde den Leerlaufstrom überproportional erhöhen, so dass er bald grösser als der zulässige Nennstrom ist. Aus diesem Grund sollten an Transformatoren nicht höhere Spannungen angelegt werden, als auf dem Typenschild angegeben ist.
Die Wärmeverluste in den beiden Wicklungen nehmen quadratisch mit dem Strom zu. Dabei ist es egal, ob Wirk- oder Blindleistung übertragen wird, der Strom heizt. Aus diesem Grund gibt man für die Nennleistung die Scheinleistung (Nennspannung mal Nennstrom) an, deren Einheit VA ist. Bei einer Belastung mit reiner Wirkleistung ist die Scheinleistung gleich gross wie die Wirkleistung.

