Es gibt Übungen für einen kleinen permanent erregten und für einen grossen fremderregten Antrieb. Zusätzlich jeweils als Option Übungen mit Reibung und Eisenverlusten.

Aufgaben Kleinantrieb (theoretisch)

Nenndaten einer permanent erregten Gleichstrommaschine: M 180 mNm, n 6876 U/min, U 24 V, I 6 A, m 500 g, J 13 mgm²

Die Eisen-, Reibungs- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1. Skizzieren Sie die skalierte Drehmoment-Drehzahl-Kennlinie dieser Maschine im Bereich von –1000 U/min bis zu 9000 U/min und zeichnen sie den Nennpunkt ein.
2. Zeichnen Sie in Skizze aus der (Aufgabe 1) die Drehmoment-Drehzahl-Kennlinie dieser Maschine an einer Spannung von 12 V.
3. Zeichnen Sie in Skizze aus der (Aufgabe 1) die Drehmoment-Drehzahl-Kennlinie dieser Maschine an einem Strom von 6 A.
4. Wie hoch die maximale dauernde Abgabeleistung beim Betrieb mit 12 V?
5. Wie hoch darf die maximale Spannung sein, damit der Motor dauernd blockiert betrieben werden kann?
6. Wie hoch ist die maximale Leistung die bei Nennspannung aus dem Antrieb kurzzeitig herausgeholt werden kann?
7. Wie gross ist der Wirkungsgrad im Nennpunkt?
8. Wie gross ist der Wirkungsgrad bei einer Belastung mit 18 mNm?
9. Wie hoch ist die Stromaufnahme bei Nennspannung und einer Drehzahl von -764 U/min?
10. Wie hoch ist die Stromaufnahme bei Nennspannung und einer Drehzahl von 8404 U/min?
11. Wie lange dauert der Hochlauf der unbelasteten Maschine am Nennstrom bis zu Nenndrehzahl?
12. Wie lange dauert der Hochlauf der unbelasteten Maschine an der Nennspannung bis zu Nenndrehzahl?

Lösung Kleinantrieb (theoretisch)

Nenndaten einer permanent erregten Gleichstrommaschine: M 180 mNm, n 6876 U/min, U 24 V, I 6 A, m 500 g, J 13 mgm²

Eisen-, Reibungs- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt

1. Skizzieren Sie die skalierte Drehmoment-Drehzahl-Kennlinie dieser Maschine im Bereich von –1000 U/min bis zu 9000 U/min und zeichnen sie den Nennpunkt ein.

Ψ = M / I = 180 mNm / 6 A = 30 mVs

Ω₀ = U / Ψ = 24 V / 30 mVs = 800 rad/s = 7640 U/min (Leerlaufdrehzahl)

P = M Ω = 180 mNm  720 rad/s = 129,6 W (mechanische Abgabeleistung)

Pe = U I = 24 V  6 A = 144 W (elektrische Aufnahmeleistung)

Pv = Pe - P = 144 W  - 129,6 W = 14,4 W (Verlustleistung)

R = Pv / I ² = 14,4 W / (6 A)² = 0,4 Ω (Verlustleistung nur im Rotorwiderstand)

I_a = U / R = 24 V / 0,4 Ω = 60 A (Anlaufstrom)

M_a = I_a Ψ = 60 A  30 mVs = 1,8 Nm (Anlaufmoment)

M_a = M Ω₀ / (Ω₀ - Ω) = 0,18 Nm  800 rad/s / (800 rad/s - 720 rad/s) = 1,8 Nm (alternativer Rechnungsweg)

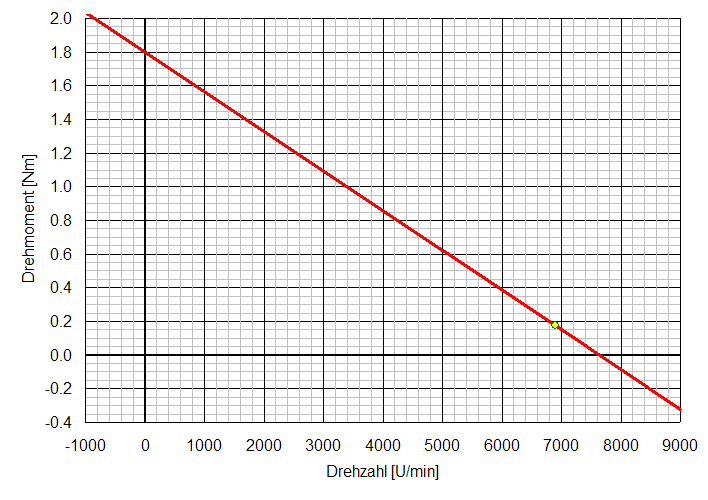
2. Zeichnen Sie in Skizze aus der (Aufgabe 1) die Drehmoment-Drehzahl-Kennlinie dieser Maschine an einer Spannung von 12 V.

Ω₀ = U / Ψ = 12 V / 30 mVs = 400 rad/s = 3820 U/min (Leerlaufdrehzahl)

M_a = (U / R) Ψ = (12 V / 0,4 Ω) 30 mVs = 0,9 Nm (Anlaufmoment)

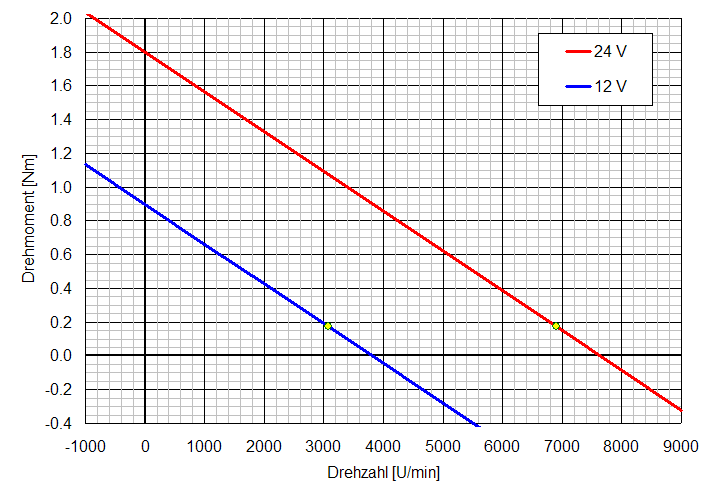
3. Zeichnen Sie in Skizze aus der (Aufgabe 1) die Drehmoment-Drehzahl-Kennlinie dieser Maschine an einem Strom von 6 A.

M = I Ψ = 6 A  30 mVs = 180 nNm (Drehmoment)

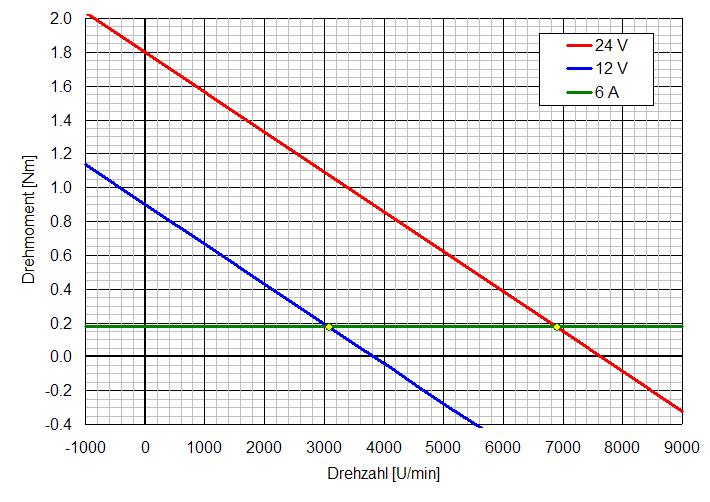
4. Wie hoch die maximale dauernde Abgabeleistung beim Betrieb mit 12 V?

Ω = Ω₀  - (Ω_{0_n} - Ω_n) = 400 rad/s - (800 rad/s  -  720 rad/s) = 320 rad/s (Drehzahl bis 12 V)

P = M  Ω = 180 mNm  320 rad/s = 57,6 W (Abgabeleistung)

5. Wie hoch darf die maximale Spannung sein, damit der Motor dauernd blockiert betrieben werden kann?

U_a = In R = 6 A  0,4 Ω = 2,4 V

6.  Wie hoch ist die maximale Leistung die bei Nennspannung aus dem Antrieb kurzzeitig herausgeholt werden kann?

P_max = M_a  Ω₀ / 4 = 1,8 Nm  800 rad/s / 4 = 360 W (Leistungsmaximum)

7. Wie gross ist der Wirkungsgrad im Nennpunkt?

η = P / Pe = 129,6 W / 144 W = 90% (Nennwirkungsgrad)

8. Wie gross ist der Wirkungsgrad bei einer Belastung mit 18 mNm?

I = M / Ψ = 18 mNm / 30 mVs = 0,6 A (Strom bei 18 mNm)

Pe = U I = 24 V  0,6 A = 14,4 W (Aufnahmeleistung bei 0,6 A)

Pv = R I² = 0,4 Ω  (0,6 A)² = 0,144 W (Verlustleistung bei 0,6 A)

η = (Pe - Pv) / Pe = (14,4 W - 0,144 W) / 14.4 W = 99% (Wirkungsgrad bei 18 mNm)

9. Wie hoch ist die Stromaufnahme bei Nennspannung und einer Drehzahl von -764 U/min?

U = R I + Ω Ψ   (Grundgleichungen)

I = (U - (Ω Ψ )) / R = (24 V - (-80 rad/s  30 mVs)) / 0,4 Ω = 66 A (Strom im Gegenstrombetrieb)

10. Wie hoch ist die Stromaufnahme bei Nennspannung und einer Drehzahl von 8404 U/min?

I = (U - (Ω Ψ )) / R = (24 V - (880 rad/s  30 mVs)) / 0,4 Ω = -6 A (Strom im Generatorbetrieb)

11. Wie lange dauert der Hochlauf der unbelasteten Maschine am Nennstrom bis zu Nenndrehzahl?

dt = (dΩ J) / M = (720 rad/s  13 mgm²) / 180 mNm = 52 ms (Hochlaufzeit)

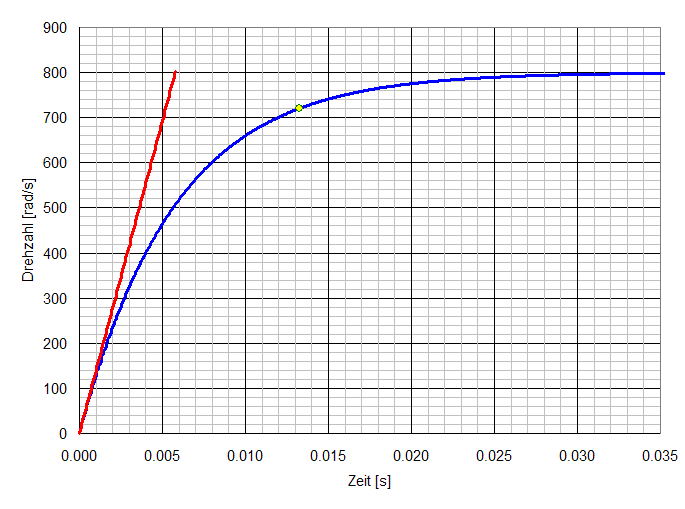
12. Wie lange dauert der Hochlauf der unbelasteten Maschine an der Nennspannung bis zu Nenndrehzahl?

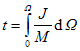
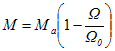
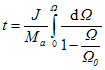
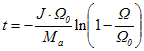
= (13 mgm²  800 rad/s / 1,8 Nm) ln(1 - (720 rad/s / 800 rad/s)) = 13,3 ms

Aufgaben Kleinantrieb (real)

Nenndaten ähnlich wie zuvor: n 6876 U/min, U 24 V, I 6 A, m 500 g, J 13 mgm² und I₀ 0,2 A (Leerlaufstrom)

Die Reibungsverluste werden berücksichtig. Die Eisen- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1. Wie hoch ist das konstante Reibungsmoment?
2. Wie hoch ist die theoretische Leerlaufdrehzahl?
3. Wie hoch ist die reale Leerlaufdrehzahl?
4. Wie hoch ist der Anlaufstrom und das Anlaufmoment?
5. Wie gross ist der Wirkungsgrad im Nennpunkt?
6. Wie gross ist der Wirkungsgrad bei einer Belastung mit 18 mNm?

Lösung Kleinantrieb (real)

Nenndaten ähnlich wie Aufgabe A: M  180 mNm, n  6876 U/min, U  24 V, I  6 A, m 500 g, J  13 mgm² und I₀  0,2 A (Leerlaufstrom)

Die Reibungsverluste werden berücksichtig. Die Eisen- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1.  Wie hoch ist das konstante Reibungsmoment?

I_m = I - I₀ = 6 A  -  0,2 A = 5,8 A (Strom für das äussere Drehmoment das Motormoment)

Ψ = M / I_m = 180 mNm / 5,8 A = 31 mVs (Flussverkettung unter Berücksichtigung der Reibung)

M_r = I₀  Ψ = 0,20 A  31 mVs = 6,2 mNm (Reibmoment im Motor, die Drehzahlachse ist um dieses Moment verschoben)

2. Wie hoch ist die theoretische Leerlaufdrehzahl?

Ω₀ = U / Ψ = 24 V / 31 mVs = 774 rad/s = 7392 U/min (Leerlaufdrehzahl)

3. Wie hoch ist die reale Leerlaufdrehzahl?

P_e = U I = 24 V  6 A = 144 W (elektrische Aufnahmeleistung)

P = M Ω = 180 mNm  720 rad/s = 129,6 W (mechanische Abgabeleistung)

P_r = M_r Ω = 6,2 mNm  720 rad/s = 4,5 W (Reibleistung)

P_i = P + Pr = 129,6 W  +  4,5 W = 134,1 W (innere mechanische Abgabeleistung)

Pv_a = Pe - P = 144 W  - 134,1 W = 9,9 W (Verlustleistung im Anker)

R = Pv_a / I ² = 9,9 W / (6 A)² = 0,28 Ω (Verlustleistung nur im Rotorwiderstand)

U = R I + Ω Ψ   (Grundgleichung)

Ω_0r = (U - (R I₀)) / Ψ = (24 V - (0,28 Ω  0,2 A) / 31 mVs = 772 rad/s = 7372 U/min (reale Leerlaufdrehzahl mit Reibung)

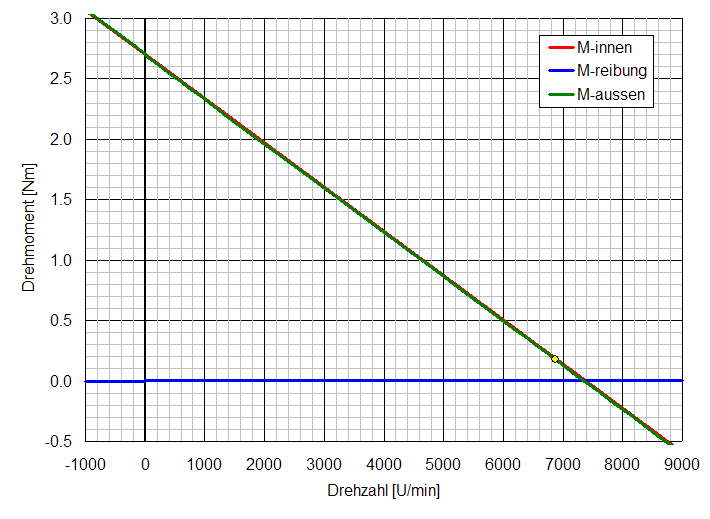
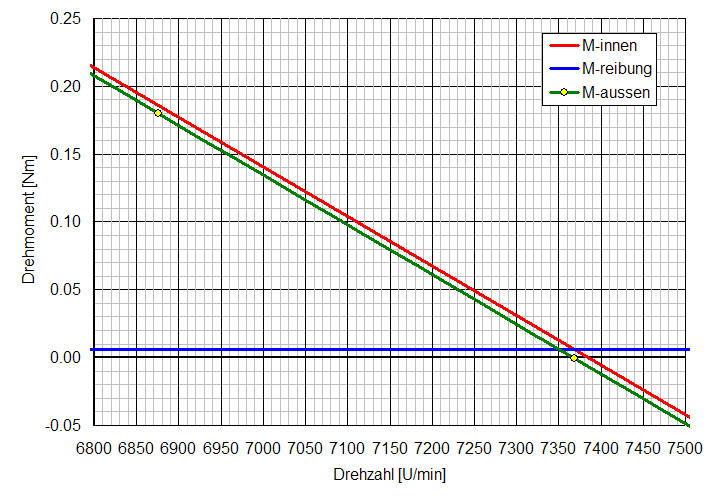
4. Wie hoch ist der Anlaufstrom und das Anlaufmoment?

I_a = U / R = 24 V / 0,28 Ω = 86 A (Anlaufstrom)

M_a = (I_a - I₀) Ψ = (86 A - 0,2 A) 31 mVs = 2,7 Nm (äusseres Anlaufmoment)

5. Wie gross ist der Wirkungsgrad im Nennpunkt?

η = P / Pe = 129,6 W / 144 W = 90%

6. Wie gross ist der Wirkungsgrad bei einer Belastung mit 18 mNm?

I = (M + Mr) / Ψ = (18 mNm + 6,2 mNm) / 31 mVs = 0,78 A (Strom bei 18 mNm äusserem Moment)

Pe = U I = 24 V  0,78 A = 18,7 W (Aufnahmeleistung bei 0,6 A)

Ω = (U - (R I)) / Ψ = (24 V - (0,28 Ω  0,78 A) / 31 mVs = 767 rad/s (Drehzahl mit 18 mNm Belastung)

P = M Ω = 18 mNm  767 rad/s = 13,8 W (mechanische äussere Abgabeleistung)

η = P / Pe = 13,8 W / 18,7 W = 74% (Wirkungsgrad bei 18 mNm äusserem Moment)

Aufgaben Grossantrieb (theoretisch)

Nenndaten einer industriellen Gleichstrommaschine: P  90 kW, n  1910 U/min, U  400 V, I  250 A, Ue  200 V, Ie  7 A, m  425 kg, J  0,64 kgm²

Die Eisen-, Reibungs- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1. Wie gross ist die Leerlaufdrehzahl und das Anlaufmoment?
2. Zeichnen Sie die Drehmoment-Drehzahl-Kennlinie bei voller und halber Erregung von –500 U/min bis zu 4500 U/min und zeichnen sie den Nennpunkt ein.
3. Wie gross ist der Wirkungsgrad im Nennpunkt?
4. Wie gross ist der Wirkungsgrad bei einer Belastung mit dem Halben Nennmoment?
5. Wie gross ist der Wirkungsgrad bei einer Belastung mit den Doppelten Nennmoment?
6. Wie gross ist der Wirkungsgrad beim Antrieb mit dem Nennmoment im Generatorquadranten?
7. Wie gross ist der Wirkungsgrad beim Antrieb bei der Belastung mit der Nennleistung bei halber Erregung?
8. Wie lange dauert etwa der Hochlauf der Maschine bis zu Nenndrehzahl, bei einer Strombegrenzung mit 250 A?
9. Wie viel Wärme entsteht im Rotor beim Hochlauf auf die Nenndrehzahl an der Nennspannung?
10. Wie gross ist das Bremsmoment im Leerlauf, wenn ein Klemmenkurzschluss an der Ankerwicklung erfolgt?
11. Wie gross ist die maximale dauernde Abgabeleistung bei 200 V Ankerspannung?
12. Wie gross ist der Wirkungsgrad bei einer Belastung mit dem Nennmoment und Betrieb mit 200 V Ankerspannung?

Lösung Grossantrieb (theoretisch)

Nenndaten einer industriellen Gleichstrommaschine: P  90 kW, n  1910 U/min, U  400 V, I  250 A, Ue  200 V, Ie  7 A, m  425 kg, J  0,64 kgm²

Die Eisen-, Reibungs- und Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt

1. Wie gross ist die Leerlaufdrehzahl und das Anlaufmoment?

M = P / Ω = 90 kW / 200 rad/s = 450 Nm

Ψ = M / I = 450 Nm / 250 A = 1,8 Vs

Ω₀ = U / Ψ 400 V / 1,8 Vs = 222 rad/s = 2120 U/min (Leerlaufdrehzahl)

P = M Ω = 180 mNm  720 rad/s = 129,6 W (mechanische Abgabeleistung)

Pe = U I = 400 V  250 A = 100 kW (elektrische Aufnahmeleistung)

Pv = Pe - P = 100 kW  -  90 kW = 10 kW (Verlustleistung)

R = Pv / I ² = 10 kW / (250 A)² = 0,16 Ω (Verlustleistung nur im Rotorwiderstand)

I_a = U / R = (400 V / 0,16 Ω) = 2,5 kA (Anlaufstrom)

M_a = I_a Ψ = 2,5 kA  1,8 Vs = 4,5 kNm (Anlaufmoment)

M_a = M Pe / Pv = 450 Nm  100 kW / 10 kW = 4,5 kNm (alternativer Rechnungsweg)

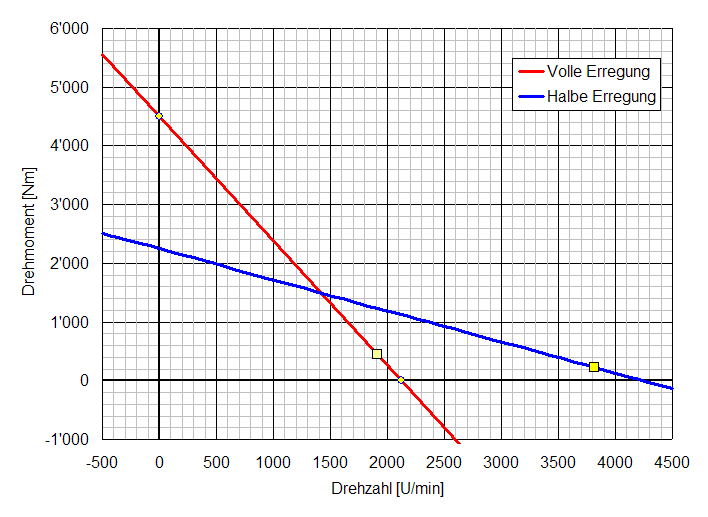
2. Zeichnen Sie die Drehmoment-Drehzahl-Kennlinie bei voller und halber Erregung von –500 U/min bis zu 4500 U/min und zeichnen sie den Nennpunkt ein.

Ω₀ = U / Ψ = 400 V / 0,9 Vs = 444 rad/s = 4240 U/min (Leerlaufdrehzahl, Psi-Halbe)

M_a = I_a Ψ = 2,5 kA  0,9 Vs = 2,25 kNm (Anlaufmoment bei Psi-Halbe)

3. Wie gross ist der Wirkungsgrad im Nennpunkt?

Per = Ue Ie = 200 V  7 A = 1,4 kW (Erregerleistung)

η = P / (Pe + Per)= 90 kW (100 kW + 1,4 kW) = 88,8% (Wirkungsgrad im Nennpunkt)

4. Wie gross ist der Wirkungsgrad bei einer Belastung mit dem halben Nennmoment?

I = M / Ψ = 225 Nm / 1,8 Vs = 125 A (Strom bei M/2)

Pe = U I = 400 V  125 A = 50 kW (Aufnahmeleistung bei 125 A)

Pv = R I² = 0,16 Ω  (125 A)² = 2,5 kW (Verlustleistung bei 125 A)

η = (Pe - Pv) / (Pe + Per) = (50 kW - 2,5 kW) / (50 kW + 1.4 kW) = 92,4% (Wirkungsgrad bei M/2)

Ω = Ω₀ - ((Ω₀ - Ω_n) M / Mn) = 222 rad/s - ((222 rad/s - 200 rad/s) 225 Nm / 450 Nm) = 211 rad/s (Drehzahl bei M/2)

P = M Ω = 225 Nm  211 rad/s = 47,5 kW (mechanische Abgabeleistung)

η = P / (Pe + Per) = 47,5 kW / (50 kW + 1.4 kW) = 92,4% (alternativer Lösungsweg)

5. Wie gross ist der Wirkungsgrad bei einer Belastung mit den Doppelten Nennmoment?

I = M / Ψ = 900 Nm / 1,8 Vs = 500 A (Strom bei 2 M)

Pe = U I 400 V  500 A = 200 kW Aufnahmeleistung bei 500 A)

Pv = R I² = 0,16 Ω  (500 A)² = 40 kW Verlustleistung bei 500 A)

η = (Pe - Pv) / (Pe + Per) = (200 kW - 40 kW) / (200 kW + 1.4 kW) = 79,4% (Wirkungsgrad bei 2M)

6. Wie gross ist der Wirkungsgrad beim Antrieb mit dem Nennmoment im Generatorquadranten?

I = M / Ψ = -450 Nm / 1,8 Vs = -250 A

Pe = U I = 400 V  -250 A = -100 kW (Abgabeleistung bei Nennmoment)

Pv = R I² = 0,16 Ω  (250 A)² = 10 kW (Verlustleistung bei Nennmoment)

η = Pe / (Pe - Pv - Per) = -100 kW (-100 kW - 10 kW - 1.4 kW) = 89,8%

7. Wie gross ist der Wirkungsgrad beim Antrieb bei Nennstrom und der Belastung mit der Nennleistung bei halber Erregung?

M = I / Ψ = 250 A  0,9 Vs = 225 Nm (Strom bei Psi-Halbe)

Ω = P / M = 90 kW / 225 Nm = 400 rad/s (Drehzahl bei Psi-Halbe)

Per = Ue Ie = 200 V  3,5 A = 0,7 A (Erregerleistung bei Psi-Halbe. Vernachlässigung der Sättigung)

η = P / (Pe - Per) = 90 kW (100 kW + 0,7 kW) = 89,4% (Wirkungsgrad bei Psi-Halbe)

8. Wie lange dauert etwa der Hochlauf der Maschine bis zu Nenndrehzahl, bei einer Strombegrenzung mit 250 A?

dt = (dΩ J) / M = (200 rad/s  0,64 kgm²) / 450 Nm = 284 ms (Hochlaufzeit)

9. Wie viel Wärme entsteht im Rotor beim Hochlauf auf die Nenndrehzahl an der Nennspannung?

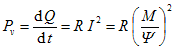
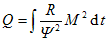
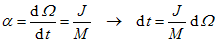
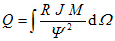
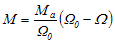
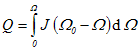
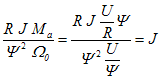
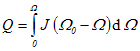
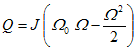
Q = 0,64 kgm² (222 rad/s 200 rad/s - (200 rad/s)² / 2 = 15,6 kJ

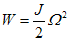
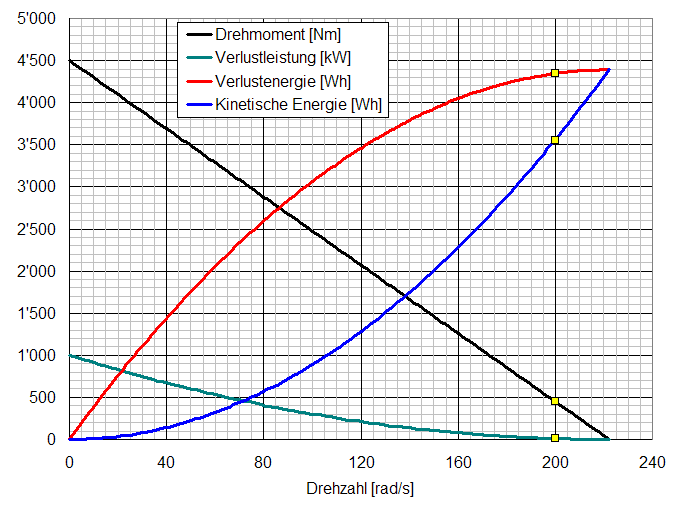
10. Wie gross ist das Bremsmoment im Leerlauf, wenn ein Klemmenkurzschluss an der Ankerwicklung erfolgt?

U = R I + Ω Ψ  (Grundgleichung)

I = (U - (Ω Ψ )) / R = (0 V - (222 rad/s  1,8 Vs)) / 0,16 Ω = -2500 A (Anlaufstrom)

M = I / Ψ = -2500 A / 1,8 Vs = -4500 Nm (Anlaufmoment)

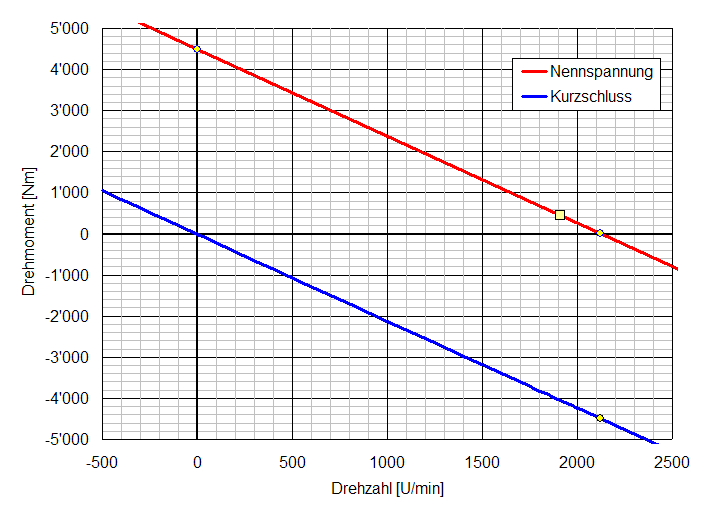
11.  Wie gross ist die maximale dauernde Abgabeleistung beim Betrieb mit 200 V Ankerspannung?

Ω₀ = U / Ψ = 200 V / 1,8 Vs = 111 rad/s = 1060 U/min (Leerlaufdrehzahl bei 200 V)

Ω = Ω₀  - (Ω_{0_n} - Ω_n) = 111 rad/s - (222 rad/s - 200 rad/s) = 89 rad/s = 850 U/min (Drehzahl bis 200 V)

P = M  Ω = 450 Nm  89 rad/s = 40 kW (Abgabeleistung)

Pe = U I = 200 V  250 A = 50 kW (Aufnahmeleistung über (Mn => In)

P = Pe - Pv = 50 kW - 10 kW = 40 kW (alternativer Rechnungsweg über Pv ~ M²)

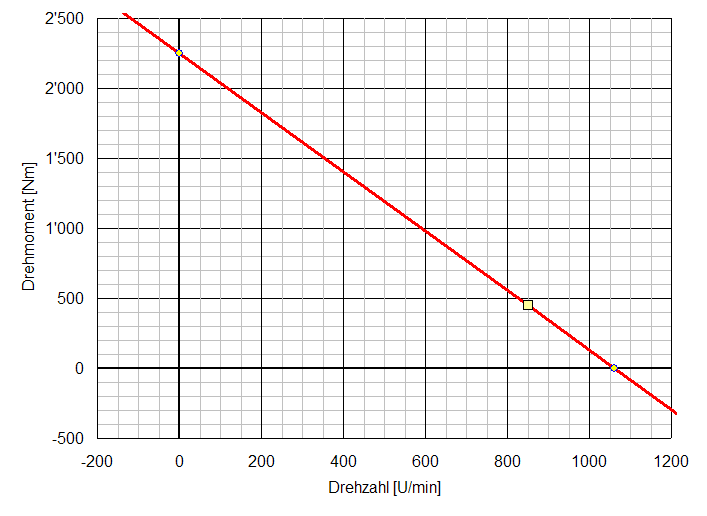
12. Wie gross ist der Wirkungsgrad bei einer Belastung mit dem Nennmoment und Betrieb mit 200 V Ankerspannung?

η = P / (Pe - Per) = 40 kW (50 kW + 1,4 kW) = 77,8%

Aufgaben Grossantrieb (real)

Nenndaten ähnlich wie zuvor: P  90 kW, n  1910 U/min, U  400 V, I  250 A, Ue  200 V, Ie  7 A, m  425 kg, J  0,64 kgm² und R  0,12 Ω, Mr  5 Nm (Reibungsmoment)

Die Eisen- und Reibungsverluste werden berücksichtig. Die Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1. Wie gross sind die Kupferverluste im Nennpunkt?
2. Wie gross sind die Reibungsverluste im Nennpunkt?
3. Wie gross sind die Eisenverluste im Nennpunkt?
4. Wie hoch ist etwa der Leerlaufstrom?
5. Wie hoch ist etwa die reale Leerlaufdrehzahl?
6. Wie hoch ist das Anlaufmoment?

Lösung Grossantrieb (real)

Nenndaten ähnlich wie zuvor: P  90 kW, n  1910 U/min, U  400 V, I  250 A, Ue  200 V, Ie  7 A, m  425 kg, J  0,64 kgm² und R  0,12 Ω, Mr  5 Nm (Reibungsmoment)

Die Eisen- und Reibungsverluste werden berücksichtig. Die Zusatzverluste, die Sättigung und Ankerrückwirkung werden vernachlässigt.

1. Wie gross sind die Kupferverluste im Nennpunkt?

Pv_Cu = R I ² = 0,12 Ω (250 A)² = 7,5 kW

2. Wie gross sind die Reibungsverluste im Nennpunkt?

Pv_r = M_r  Ω = 5 Nm  200 rad/s = 1,0 kW

3. Wie gross sind die Eisenverluste im Nennpunkt?

Pe = U I = 400 V  250 A = 100 kW (elektrische Aufnahmeleistung)

Pv = Pe - P = 100 kW - 90 kW = 10 kW (gesamte Verlustleistung)

Pv_Fe= Pv - Pv_Cu - Pv_r = 10 kW - 7,5 kW - 1 kW = 1,5 kW

4. Wie hoch ist etwa der Leerlaufstrom?

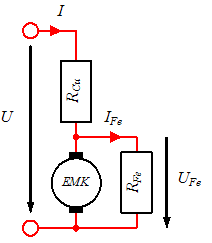
U_FE = Ω Ψ = U - (R I ) = 400 V - (0,12 Ω  250 A) = 370 V (induzierte Spannung (EMK) im Nennbetrieb)

R_Fe = U_FE ² / Pv_Fe (370 V)² / 1,5 kW = 91 Ω (Ersatzwiderstand für die Eisenverluste)

I_Fe = U_FE / R_Fe = 370 V / 91 Ω = 4,1 A (Nennstrom durch den Ersatzwiderstand für die Eisenverluste)

I_a = I - I_r = 250 A - 4,1 A = 245,9 A (Strom durch die EMK)

I_a = (P + P_r) / U_Fe = (90 kW + 1 kW) / 370 V = 245,9 A (Kontrollrechnung für Strom durch die EMK)

Ψ = (M + M_r) / Ia = (450 Nm + 5 Nm) / 245,9 A = 1,85 Vs (Flussverkettung mit innerem Moment und Strom)

I_r = M_r / Ψ = 5 Nm / 1,85 A = 2,7 A (Leerlaufstrom in der EMK)

I_{0_1} = I_r + I_Fe = 2,7 A + 4,1 A = 6,8 A (1. Nähung für den Leerlaufstrom in den Motor)

U_{FE_1} = U - (R  I_{0_1}) = 400 V - (0,12 Ω  6,8 A) = 399 V (induzierte Spannung (EMK) im Leerlauf)

I_{Fe_1} = U_FE / R_Fe = 399 V / 91 Ω = 4,4 A (Nennstrom durch den Ersatzwiderstand für die Eisenverluste)

I₀ = I_r + I_Fe 2,7 A + 4,4 A = 7,1 A (Leerlaufstrom)

5. Wie hoch ist etwa die reale Leerlaufdrehzahl?

Ω₀ = U / Ψ = 400 V / 1,85 Vs = 216,2 rad/s = 2065 U/min (theoretische Leerlaufdrehzahl)

dΩ = (Ω₀ - Ω_n) M_r / (M + M_r) = (216,2 rad/s - 200 rad/s) 5 Nm / (450 Nm + 5 Nm) = 0,3 rad/s (Drehzahlabfall durch die Reibung)

Ω_0r = Ω₀ - dΩ = 216,2 rad/s - 0,3 rad/s = 215,9 rad/s = 2062 U/min (reale Leerlaufdrehzahl)

6. Wie hoch ist das Anlaufmoment?

I_a = U / R = (400 V / 0,12 Ω) = 3,33 kA (Anlaufstrom)

M_a = I_a Ψ = 3,3 kA  1,85 Vs = 6,2 kNm