Bei Gasen gibt es feste Beziehungen zwischen Druck, Volumen und Temperatur, wenn diese weit genug von der Veränderung des Aggregatzustandes (Verdampfung, Kondensation) entfernt sind.
| Grösse | Beziehung, Symbol |
Einheit | Bemerkungen |
|---|---|---|---|
| Gasgleichung ideal | \(p v = R T\) | J | Beziehung für ideale Gase, genügt für einfache Berechnungen |
| Druck | \(p\) | Pa |
Absolutdruck, der Normatmosphärendruck ist 1.013 bar = 101'300 Pa |
| Spezifisches Volumen | \(v\) | m³/kg | Kehrwert des spezifischen Gewichtes |
| Temperatur | \(T\) | K | Absolute Temperatur (0 °C = 273,15 K) |
| Gaskonstante | \(R\) | J/kgK | Luft hat 287 J/kgK |
| Gasgleichung real | \(p v = Z R T\) | J | Beziehung für reale Gase |
| Realgasfaktor | \(Z\) | - |
etwa 1, Korrekturwert für reale Gase (druck- und temperaturabhängig) ZLuft 1 bar, 0 °C = 1.00, 100 bar, 0 °C = 0.97 und bei 100 °C = 1.02 |
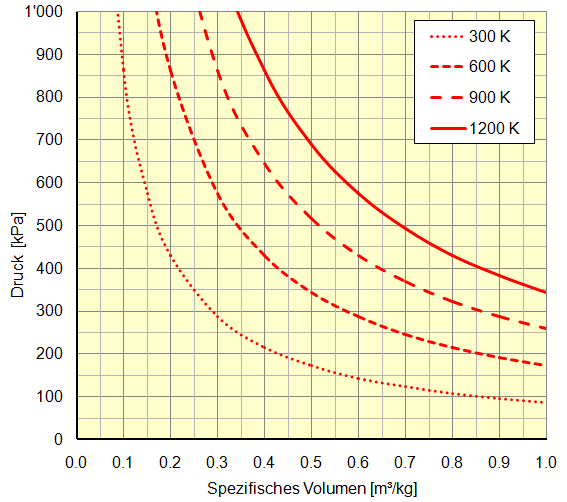
Bei der Darstellung im Druck-Volumen-Diagramm liegen konstante Temperaturen auf Hyperbeln:
Enthalpie und Entropie
In der Thermodynamik ist das Mass für den Energieinhalt eines Stoffes die Enthalpie und ein Mass für die Umkehrbarkeit (Reversibilität) von Vorgängen, die Entropie. Vereinfacht kann man die Entropie auch ein Mass für die Unordnung nennen.
| Grösse | Beziehung, Symbol |
Einheit | Bemerkungen |
|---|---|---|---|
| Enthalpie | \(h_2 = h_1 + q_{12} + w_{12}\) | J/kg | Energieerhaltungssatz, Index 1 für Ausgangslage, Index 2 für die Endlage |
| Entropie | \(s_2 = s_1 + c_{p,v} \ln (T_2/T_1) + R \ln (v_2/v_1)\) | J/kgK | Index 1 für Ausgangslage, Index 2 für die Endlage |
| Wärmzufuhr | \(q_{12} = c_{p,v} (T_2 - T_1)\) | J/kg | Der Wert für die Wärmekapazität hängt von der Druck- beziehungsweise Volumenveränderung ab |
| Mechanische Arbeit | \(w_{12} =\int^2_1(p v)\) | J/kg | Integral von Druck über spezifisches Volumen (Kraft über Weg) |
| Wärmekapazität isobar | \(c_p\) | J/kgK | Wärmekapazität bei einer Erwärmung mit konstanten Druck, Luft hat 1000 J/kgK, bei realen Gasen ist die Wärmekapazität temperaturabhängig |
| Wärmekapazität isochor | \(c_v = c_p - R\) | J/kgK | Wärmekapazität bei einer Erwärmung mit konstanten Volumen, Luft hat 713 J/kgK, bei realen Gasen ist die Wärmekapazität temperaturabhängig |
| Adiabatenexponent | \(\kappa = c_p/c_v = (f + 2) / f\) | - | auch Isentropenexponent genannt, temperaturabhängig (He = 1.66, O_2 = 1.4, CO_2 = 1.3) |
| Freiheitsgrad | \(f = 2 / (\kappa - 1)\) | - |
Freiheitsgraden des Gasmoleküls: Translation 3, Rotation 0, 2 oder 3, Schwingung 0 bis über 10 (nimmt mit der Molekülgrösse und Temperatur zu) |
Der Begriff "adiabat" steht für keinen Wärmeaustausch mit der Umgebung (gute Wärmedämmung).
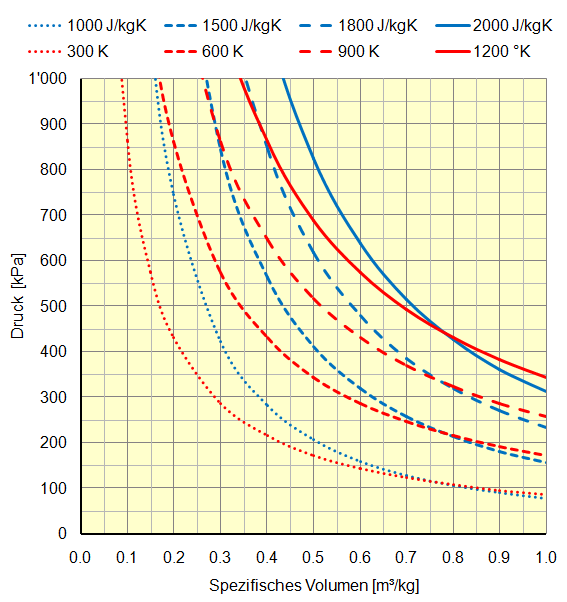
Bei der Darstellung im Druck-Volumen-Diagramm kommen zu den Kurven konstanter Temperaturen die der Entropie dazu:
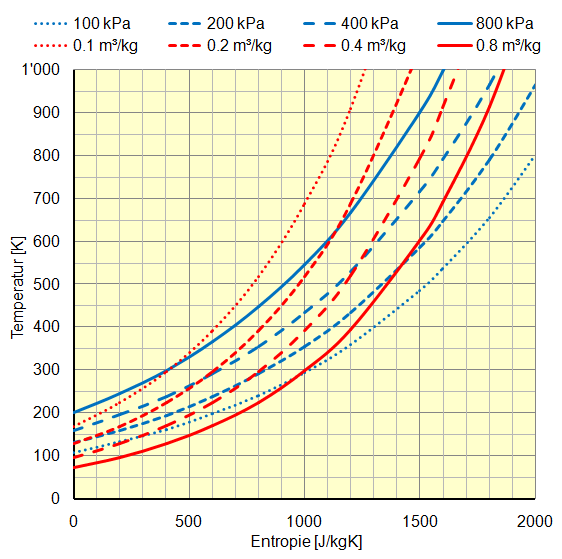
Mit der Entropie gibt es zusätzlich die Darstellung im Temperatur-Entropie-Diagramm:
Zustandsänderungen
In der Thermodynamik gibt es folgende Definitionen von Zustandsänderungen für ideale Gase:
| Begriff | Beziehung |
Einheit | Bemerkungen |
|---|---|---|---|
| Isochor | \(v_1 = v_2\) | m³/kg | Zustandsänderung bei konstantem Volumen |
| \(p_1/p_2 = T_1/T_2\) | - | Die Druckverhältnis entspricht dem Temperaturverhältnis | |
| \(q_{12} = c_v (T_2 - T_1)\) | J/kg | Die Erforderliche Wärme entspricht der Temperaturveränderung | |
| \(w_{12} = 0\) | J/kg | Die mechanische Arbeit (geschlossenes System) ist Null | |
| \(w_{t12} = v (p_2 - p_1)\) | J/kg | Die technische Arbeit (offenes System) entspricht der Druckveränderung | |
| \(s_2 - s_1 = c_v \ln (T_2/T_1)\) | J/kgK | Die Entropieänderung entspricht dem Logarithmus der Temperaturverhältnis | |
| Isobar | \(p_1 = p_2\) | Pa | Zustandsänderung bei konstantem Druck |
| \(v_1/v_2 = T_1/T_2\) | - | Die Druckverhältnis entspricht der Volumenverhältnis | |
| \(q_{12} = c_p (T_2 - T_1)\) | J/kg | Die erforderliche Wärme entspricht der Temperaturveränderung | |
| \(w_{12} = p (v_2 - v_1)\) | J/kg | Die mechanische Arbeit entspricht der Volumenveränderung | |
| \(w_{t12} = 0\) | J/kg | Die technische Arbeit ist Null | |
| \(s_2 - s_1 = c_p \ln (T_2/T_1)\) | J/kgK | Die Entropieänderung entspricht dem Logarithmus der Temperaturverhältnis | |
| Isotherm | \(T_1 = T_2\) | K | Zustandsänderung bei konstanter Temperatur |
| \(p_1 v_1 = p_2 v_2\) | - | Das Produkt Druck mal Volumen bleibt konstant | |
| \(q_{12} = p_1 v_1 \ln (p_2/p_1)\) | J/kg | Die Erforderliche Wärme entspricht dem Logarithmus der Druckverhältnis | |
| \(w_{12} = w_{t12} = - q_{12}\) | J/kg | Die mechanische und technische Arbeit entspricht der Wärme | |
| \(s_2 - s_1 = R \ln (v_2/v_1)\) | J/kgK | Die Entropieänderung entspricht dem Logarithmus der Volumenverhältnis | |
| Isentrop | \(s_1 = s_2\) | J/kgK | Zustandsänderung bei konstanter Entropie |
| \(p_1/p_2 = (v_2/v_1)^\kappa\) | - | Das Produkt Druck mal Volumen hoch Adiabtenkoeffizient bleibt konstant | |
| \(v_2/v_1 = (T_1/T_2)^{1/(\kappa-1)}\) | - | Volumenverhältnis zu Temperaturverhältnis | |
| \(T_2/T_1 = (p_2/p_1)^{(\kappa-1)/\kappa}\) | - | Temperaturverhältnis zu Druckverhältnis | |
| \(q_{12} = 0\) | J/kg | Einen Prozess ohne Wärmeaustausch nennt man adiabat | |
| \(w_{12} = R / (\kappa - 1) (T_2 - T_1)\) | J/kg | Die mechanische Arbeit entspricht der Temperaturdifferenz | |
| \(w_{12} = 1 / (\kappa - 1) (p_2 v_2 - p_1 v_1)\) | J/kg | Die mechanische Arbeit entspricht der Veränderung des Produktes aus Druck mal Volumen | |
| \(w_{12} = 1 / (\kappa - 1) p_1 v_1 ((p_2/p_1)^{(\kappa-1)/\kappa} - 1)\) | J/kg | Die mechanische Arbeit entspricht dem Druckverhältnis | |
| \(w_{t12} = \kappa w_{12}\) | J/kg | Die technische Arbeit ist die mechanische Arbeit mal der Adiabatenkoeffizient | |
| \(s_2 - s_1 = R \ln (v_2/v_1)\) | J/kgK | Die Entropieänderung entspricht dem Logarithmus der Volumenverhältnis | |
| polytrop | \(v_2/v_1 = (p_1/p_2)^{1/n} = (T_1/T_2)^{1/(n-1)}\) | Beliebige Zustandsänderung | |
| \(n\) | - | Polytropenkoeffizient: isochor n = ∞, isobar n = 0, isotherm n = 1, isotrop n = \(\kappa\), bei realen Verdichtungen und Expansionen liegt n etwas unter \(\kappa\) |
|
| \(q_{12} = c_v (n - \kappa) (T_2 - T_1) / (n - 1)\) | J/kg | Die erforderliche Wärme entspricht der Temperaturveränderung | |
| \(w_{12} = R (T_2 - T_1) / (n - 1)\) | J/kg | Die mechanische Arbeit entspricht der Temperaturdifferenz | |
| \(w_{12} = (p_2 v_2 - p_1 v_1) / (n - 1)\) | J/kg | Die mechanische Arbeit entspricht der Veränderung des Produktes aus Druck mal Volumen | |
| \(w_{12} = p_1 v_1 ((p_2/p_1)^{(n-1)/n} - 1) / (n - 1)\) | J/kg | Die mechanische Arbeit entspricht dem Druckverhältnis | |
| \(w_{t12} = n w_{12}\) | J/kg | Die technische Arbeit ist die mechanische Arbeit mal der Polytropenkoeffizient | |
| \(s_2 - s_1 = c_v \ln (p_2/p_1) + c_p \ln (v_2/v_1)\) | J/kgK | Die Entropieänderung entspricht dem Druckverhältnis und dem Volumenverhältnis |
Die mechanische Arbeit w ist die mechanische Arbeit in einem geschlossenen System, die technische Arbeit wt ist die Arbeit in einem offenen System (Pumpe, Turbine ...).
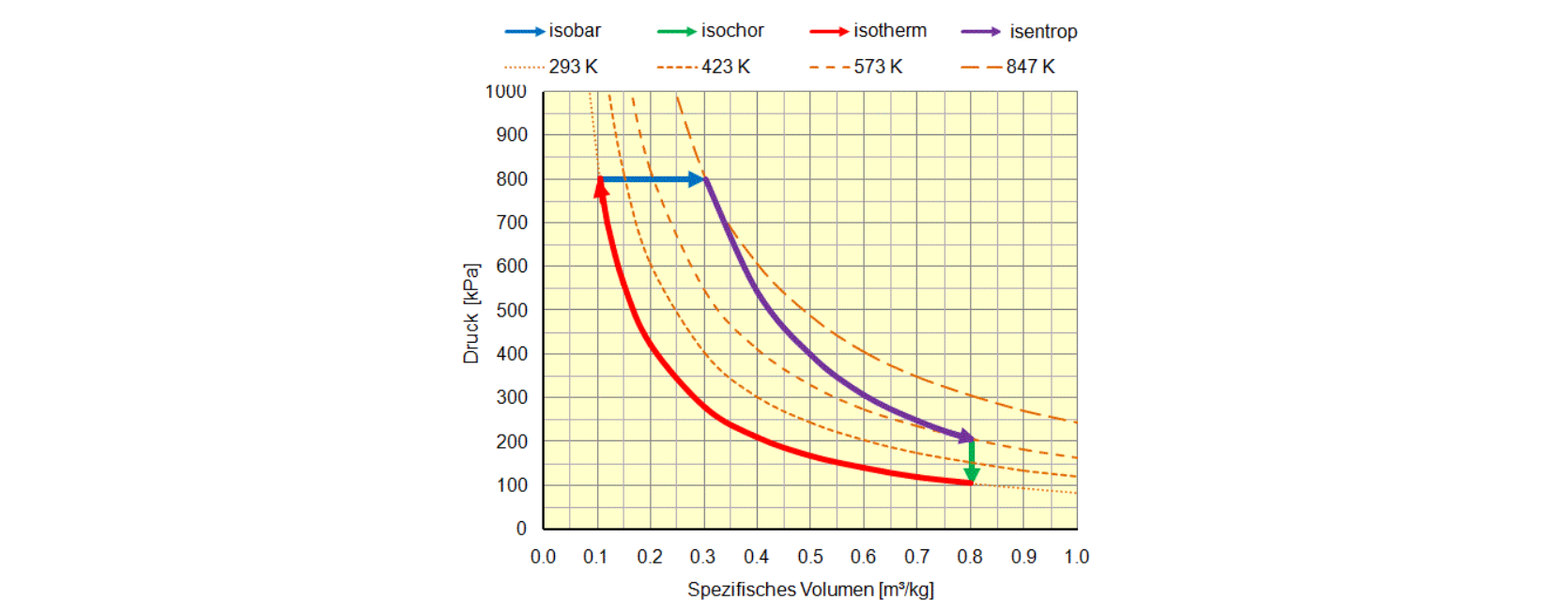
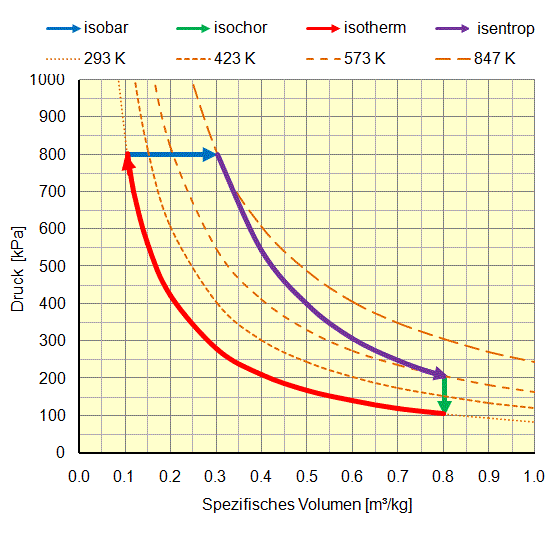
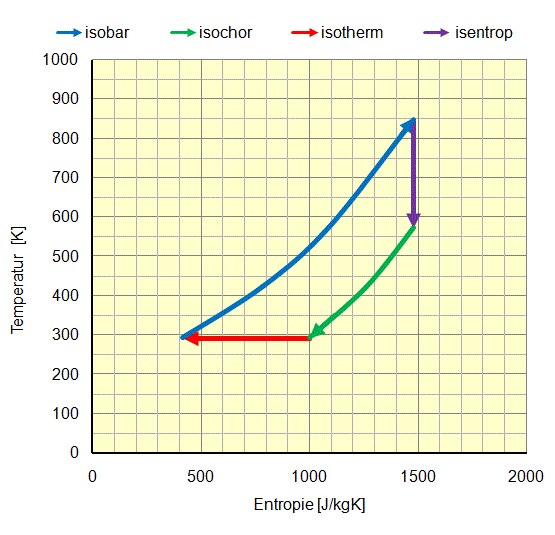
Im folgenden Beispiel werden folgende Veränderungen von Luft in einem geschlossenen System Luft im p-v und T-s Diagrammen theoretisch dargestellt:
- Isotherme Verdichtung (rot): Luft wird durch Kompression vom Normalzustand 100 kPa (1 bar absolut) und 0,8 m³/kg 293 K (20 °C) unter konstanter Temperatur auf einen Druck von 800 kPa (8 bar absolut) verdichtet. Dabei nimmt das spezifische Volumen auf 0,1 m³/kg ab. Die erforderliche mechanische Arbeit beträgt rund 170 kJ, was auf einem Temperaturniveau von 293 K (20 °C) als Wärme an die Umgebung abgegeben wird. Ausgehend von einer Startgrösse für die Entropie von 1000 kJ/kgK sinkt diese auf rund 400 kJ/kgK.
- Isobare Expansion (blau): Luft wird durch Erhitzung von 800 kPa (8 bar absolut), 0,1 m³/kg und 293 K (20 °C) bei konstantem Druck auf ein spezifisches Volumen von 0,3 m³/kg und eine Temperatur von 847 K (575 °C) expandiert. Die erforderliche Wärme beträgt etwa 560 kJ/K. Die gewonnene mechanische Arbeit aus der Volumenvergrösserung beträgt 160 kJ/kg. Die Entropie nimmt von 400 kJ/kgK auf 1500 kJ/kgK zu.
- Isentrope Expansion (violett): Luft wird durch Expansion von 800 kPa (8 bar absolut), 0,3 m³/kg und 847 K (575 °C) ohne Wärmeaabgabe auf 200 kPa (2 bar absolut), 0,8 m³/kg und 573 K (300 °C) expandiert. Die gewonnene mechanische Arbeit beträgt rund 200 kJ/kg. Die Entropie bleibt mit 1500 kJ/kgK konstant.
- Isochore Druckabnahme (grün): Luft wird durch Kühlung (oder Austausch) von 200 kPa (2 bar absolut), 0,8 m³/kg und 573 K (300 °C) auf ein Druckniveau von 100 kPa (1 bar absolut) bei 0,8 m³/kg und 293 K (20 °C) auf die Ausgangsgrössen zurückgebracht. Die abgeführte Wärme beträgt rund 200 kJ. Die Entropie nimmt von 1500 kJ/kgK auf 400 kJ/kgK ab.
Zusammenfassung für diesen theoretischen Kreisprozess für 1 kg Luftumsatz:
- Die zugeführte Wärmemenge beträgt 560 kJ, die abgeführte 370 kJ, was eine Nettowärmezufuhr von 190 kJ ergibt.
- Die zugeführte mechanische Arbeit beträgt 170 kJ, die abgegebene 360 kJ, was eine Nettoarbeitsabgabe von 190 kJ ergibt. Die Arbeitsabgabe entspricht auch der Fläche, welche im p-v und T-s von diesem Kreisprozess aufgespannt wird.
- Weil in einem Kreisprozess der Ausgangspunkt wieder erreicht wird, muss die Nettowärmezuführ gleichgross sein wie die Nettoarbeitsabgabe.
- Der Wirkungsgrad für diese Wärmekraftmaschine ist das Verhältnis von Nettoarbeitsabgabe zur Wärmezufuhr und beträgt 190 kJ durch 560 kJ gleich 34%. Wenn die Abwärme bei der isochoren Druckverminderung bis auf 20 °C genutzt wird, kommen noch 200 kJ Wärmeenergie dazu und der Gesamtwirkungsgrad erhöht sich auf 70%
- Der theoretisch maximale Wirkungsgrad für eine Wärmekraftmaschine (Carnotwirkungsgrad) rechnet sich aus der Differenz der höchsten Temperatur zur Umgebungstemperatur durch die höchste Temperatur. Bei diesem Beispiel wären das 847 K minus 293 K durch 847 K, was 65% ergibt.
Gaswerte
In der untenstehenden Tabelle sind die Werte von einigen ausgesuchten Gasen bei 0°C und 100 kPa aufgeführt:
| Gasart | \(M\) | \(v\) | \(R\) | \(c_p\) | \(c_v\) | \(\kappa\) | |
|---|---|---|---|---|---|---|---|
| kg/kmol | m³/kg | kJ/kgK | kJ/kgK | kJ/kgK | - | ||
| Wasserstoff | H2 | 2.02 | 11.126 | 4.124 | 14.210 | 10.090 | 1.41 |
| Helium | He | 4.00 | 5.603 | 2.077 | 5.194 | 3.117 | 1.66 |
| Methan | CH4 | 16.04 | 1.395 | 0.518 | 2.158 | 1.640 | 1.32 |
| Ethin | C2H2 | 26.04 | 0.851 | 0.319 | 1.629 | 1.310 | 1.23 |
| Stickstoff | N2 | 28.01 | 0.800 | 0.297 | 1.040 | 0.743 | 1.40 |
| Luft | N2, O2 | 28.96 | 0.773 | 0.287 | 1.004 | 0.718 | 1.40 |
| Ethan | C2H6 | 30.07 | 0.737 | 0.277 | 1.654 | 1.377 | 1.20 |
| Sauerstoff | O2 | 32.00 | 0.700 | 0.260 | 0.915 | 0.655 | 1.40 |
| Kohlendioxid | CO2 | 44.01 | 0.506 | 0.189 | 0.818 | 0.628 | 1.30 |
| Butan | C4H10 | 58.12 | 0.366 | 0.143 | 1.623 | 1.480 | 1.10 |
| Schwefeldioxid | SO2 | 64.07 | 0.342 | 0.130 | 0.607 | 0.477 | 1.27 |